29 – 36 Determine os valores máximo e mínimo absolutos de f no conjunto D.34 -fx ,y = x y 2 , D = x , yx ≥ 0 ,y ≥ 0 ,x 2 + y 2 ≤ 3 }

O máximo absoluto de f em D é f 1 , 2 = 2 e o mínimo absoluto é0 , que ocorre em todos os pontos de L 1 e L 2 .

Enunciado

Faaala, galera. Tudo certo? Nessa questão nós temos a seguinte função e domínio:

;

A partir disso, queremos determinar os valores máximo e mínimo absolutos de no seu domínio.

Esse domínio pode ser visto na imagem abaixo:

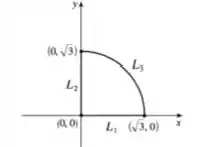
Pelo domínio temos que ele é delimitado por esse quarto de uma circunferência.

Para determinar os valores máximo e mínimo absolutos de uma função contínua fem um conjunto fechado e limitado D:

1. Determine os valores de nos pontos críticos de em .

2. Determine os valores extremos de na fronteira de .

3. O maior dos valores dos passos 1 e 2 é o valor máximo absoluto; o menor desses valores é o valor mínimo absoluto.

Tranquilo? Vamos lá então.

Como queremos os pontos de máximo e mínimo, precisamos achar as derivadas parciais e os pontos críticos, isto é, os pontos onde elas se anulam.

Lembrando que as derivadas serão

Note que se , temos que logo não há ponto crítico no interior de .

Como não há ponto critico no interior do nosso domínio, vamos avaliar os lados:

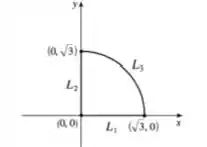
Em , e .

Em e

Em .

Pegando para teremos

logo

então,

Essa derivada se anula para , e só nos importa que está em .

O valor máximo é e o valor mínimo absoluto é , que ocorre em (nos extremos).

Assim, o máximo absoluto de em é e o mínimo absoluto é, que ocorre em todos os pontos de e .

O máximo absoluto de em é e o mínimo absoluto é, que ocorre em todos os pontos de e .