8. Considere a função g(x, y) = onde f (u) é uma função de uma variável real a valores reais, contínua em [a, b], 0 ≤ a a 2   ≤   x 2   +   y 2   ≤   b 2 e 0 ≤ z ≤ g(x, y)}

1. Verifique que B é gerado pela rotação em torno do eixo z do conjunto.

Podemos observar isso por argumento geométrico. Temos Essas duas curvas que expressão os limites de z

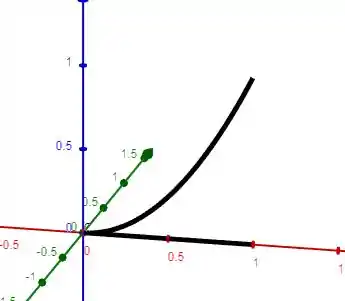
Seguindo as regras de

O que por motivos didáticos vamos supor que

Rotacionando essa superfície formada entre as curvas teremos

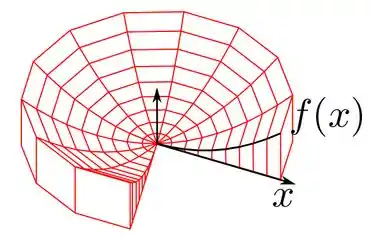
Que se formos definir formalmente esse conjunto seria

Que é justamente o que queríamos propor no enunciado. Terminamos por aqui. Te vejo na próxima resolução

: )