Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.2 - Ex. 7

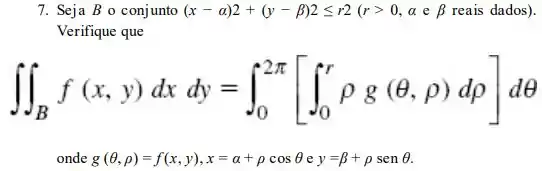
Passo 1

Através da integral dupla, tem-se:

int int_B f (x , y) d x d y

= int_a^b [int_(c (y))^(d (y)) f (x , y) d x] d y = int_c^d [int_(a (x))^(b (x)) f (x , y) d y] d x

Neste caso, B é dado no enunciado como um círculo deslocado da origem de raio r . Visto que alpha > 0 e beta > 0 :

- r <= x - alpha <= r -> - r + alpha <= x <= r + alpha

- r <= y - beta <= r -> - r + beta <= y <= r + beta

Assim, fazendo:

x - alpha = rho c o s theta

y - beta = rho s e n theta

Tem-se que:

f (x , y) = g (rho , theta)

Pretende-se determinar o resultado da transformação:

(x , y) = phi (rho , theta)

Dada por:

d x d y = |(del (x , y))/(del (rho , theta))| d rho d theta

Então:

(del (x , y))/(del (rho , theta)) = |[[(del x)/(del rho),(del x)/(del theta)],[(del y)/(del rho),(del y)/(del theta)]]| = |[[c,o,s,theta,-,rho,s,e,n,theta],[s,e,n,theta,rho,c,o,s,theta]]| = rho (c o s^2 theta + s e n^2 theta)

(del (x , y))/(del (rho , theta)) = rho

Portanto:

d x d y = rho d rho d theta

Passo 2

Agora, deve se determinar o conjunto B_rho theta , onde B = phi (B_rho theta) . Assim, o novo conjunto será dado através do limite do conjunto original. Visto que B é uma elipse de eixos a e b , então as novas variáveis serão dadas por:

(x - alpha)^2 + (y - beta)^2 = r^2 -> (rho c o s theta)^2 + (rho s e n theta)^2 = r^2 :. rho = r

Com isso:

0 <= rho <= r

E

0 <= theta <= 2 pi

Dessa forma, tem-se:

B_rho theta = {(rho , theta) in R^2 | 0 <= rho <= r e 0 <= theta <= 2 pi}

Passo 3

Logo, a integral será dada por:

int_0^b [int_0^a f (x , y) d x] d y = int_0^(2 pi) [int_0^r g (rho , theta) rho d rho] d theta

Que pode ser reorganizado em:

= int_0^(2 pi) [int_0^r rho g (rho , theta) d rho] d theta

Portanto, conclui-se que:

int int_B f (x , y) d x d y = int_0^(2 pi) [int_0^r rho g (rho , theta) d rho] d theta

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∫ ∫ B f x ,y d x d y sendo dados:
Calcule ∫ ∫ B f x ,y d x d y sendo dados:
Utilizando integral dupla, calcule a área do conjunto B dado.
Utilizando integral dupla, calcule a área do conjunto B dado.
Utilizando integral dupla, calcule a área do conjunto B dado.