Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 44
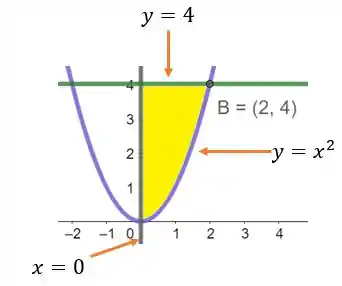
Esboce a região de integração e mude a ordem de integração.
Passo 1
E aí, futuro cientista! Preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!
Hoje vamos aprender a identificar e esboçar a região de integração, além de mudar a ordem de integração.
Nosso primeiro passo é identificar com que tipo de região estamos lidando: se é do tipo I ou do tipo II. Depois disso, vamos esboçá-la e mudar a ordem da integral. Mudando a ordem de integração, podemos simplificar a resolução de integrais duplas, tornando o processo mais fácil dependendo da função e dos limites envolvidos.
Lembre-se de que podemos fazer isso sempre que tivermos uma integral dupla com limites que indicam uma região complexa ou quando a ordem original dificulta a integração.
Para começar, precisamos identificar a região de integração. Dado que a integral é:
Podemos ver que estamos integrando inicialmente em . Isso significa que estamos trabalhando com uma região do tipo I, onde os limites de são funções de .
A região do tipo I é descrita pelos limites:
Passo 2
Agora que determinarmos a nossa região, podemos esboçá-la para visualizar melhor.
- A curva = é uma parábola que se abre para cima.
- A reta é uma linha horizontal.
Os limites de variam de a . Vamos desenhar a região no plano :
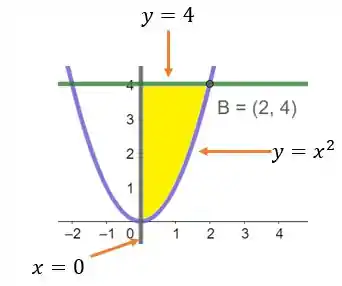
Passo 3
Agora que esboçamos a região de integração, vamos escrevê-la como uma região do tipo II.
Para a região do tipo II, a região é limitada lateralmente por curvas e acima e abaixo por retas horizontais. A descrição da região é:
- À esquerda pela reta
- À direita pela curva
- Abaixo por
- acima por
Portanto, a integral correspondente é dada por:
Resposta
