Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.2 - Ex. 30
- Determine o volume do sólido limitado pela superfície e pelos planos , , , e .
- Use um computador para desenhar o sólido.
Passo 1
Nesse exercício queremos calcular o volume do sólido que é limitado pela superfície e no eixo e pelo retângulo , no plano .
Desta forma para calcular o volume deste sólido precisamos calcular uma integral dupla.
Passo 2
a) Calculando o volume:
Passo 3
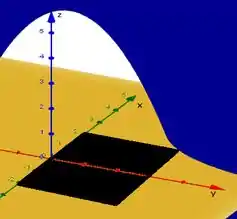
b) O sólido no qual estamos calculando o vomue está situado abaixo da superfície em azul que é dada pela equação e acima do retângulo .
Resposta
a) O volume é .
Exercícios de Livros Relacionados
Utilize uma calculadora programável ou computador (ou o comando de soma de um SCA) para estimar ∬ R1 + x e - y d A onde R = 0 ,1 × 0 ,1 . Utilize a Regra do Ponto Médio com os seguintes números de qua
A integral ∬ R9 - y 2 d A , onde R = 0 ,4 × 0 ,2 , representa o volume de um sólido. Esboce o sólido.
Estime o volume do sólido que está abaixo da superfície z = x y e acima do retângulo R = x , y | 0 ≤ x ≤ 6 ,0 ≤ y ≤ 4 Utilize a soma de Riemann com m = 3 , n = 2 e tome como ponto amostral o canto sup
Mostre que ∬ ∂ 2 f ( x , y ) ∂ x ∂ y d x d y Sobre o retângulo x 0 ≤ x ≤ x 1 ,y 0 ≤ y ≤ y 1 , é f x 1 , y 1 - f x 0 , y 1 - f x 1 , y 0 + f ( x 0 , y 0 )
Suponha que ƒ(x, y) possa ser escrita como um produtoƒ(x, y) = F(x)G(y) de uma função de x e uma função de y.Então a integral de ƒ sobre o retângulo R: a ≤ x ≤ b, c ≤y ≤ d pode ser calculada também co