Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.1 - Ex. 14
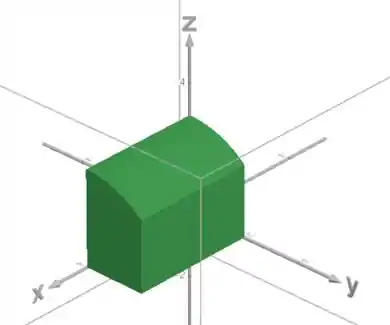
A integral , onde , representa o volume de um sólido. Esboce o sólido.
Passo 1
Oi pessoal, tudo bem?
Nessa questão a gente precisa esboçar o sólido que essa integral representa!
Então vamos lembrar como a integral se relaciona com um sólido?
Bom, sempre que nós temos uma integral:
Ela é o volume do sólido entre a superfície e o plano , limitado no domínio , que é uma região do plano .
Então nosso problema vai se dividir em dois: determinar quem é esse domínio , e determinar quem é a superfície . Assim, conseguimos esboçar o sólido.
Passo 2
A primeira coisa a analisar é a nossa região . Ela é um retângulo , ou seja, com e :
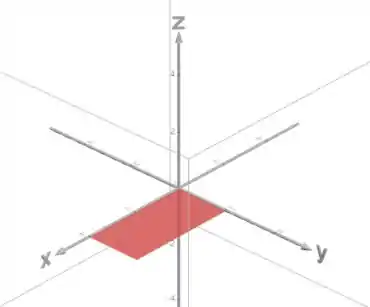
Agora precisamos ver quem é a superfície
Passo 3
A superfície vai ser:
Essa superfície é um cilindro de raio , ao longo do eixo . Mas percebe uma coisa: como a nossa expressão inicial era , a gente ta falando só da parte da superfície onde , porque uma raiz quadrada nunca pode ser negativa! Então vai ficar assim:
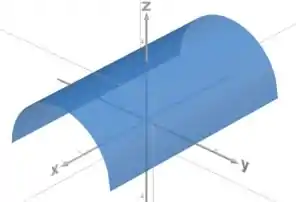
Passo 4
Agora vamos pegar só a parte do cilindro que está no domínio :
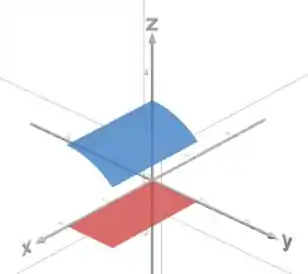
Pra fechar, o sólido é toda a região entre essas duas superfícies:
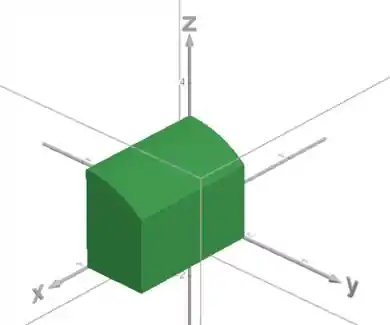
Resposta
