Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.1 - Ex. 15
Utilize uma calculadora programável ou computador (ou o comando de soma de um SCA) para estimar.
onde . Utilize a Regra do Ponto Médio com os seguintes números de quadrados de tamanhos iguais: e .
Passo 1
Fala, pessoal! Tudo joia?
A questão pede para que a gente estime o valor da integral dupla:
Na região abaixo da função definida pelo retângulo .
Vamos usar o software Maple para realizar esses cálculos.
Bora lá!
Passo 2
No software Maple imputamos a função:
Nesse software colocamos os comandos em forma de código:
middlesum (middlesum (f, x=0. .1,m),
y=0..1,m);
Aqui, é o número de quadrados que o enunciado pede que a gente varie com os valores de: e .
Passo 3
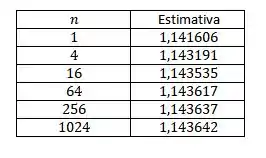
Os valores de que imputamos no Maple e seus respectivos valores para a integral:
Estão na tabela abaixo:
Resposta
Exercícios de Livros Relacionados
A integral ∬ R9 - y 2 d A , onde R = 0 ,4 × 0 ,2 , representa o volume de um sólido. Esboce o sólido.
Se f é uma função constante, f (x , y) = k , e R = [a , b] xx [c , d] , mostre que∬_R^() k d A = k ( b - a ) ( d - c )
Use o resultado do Exercício 17 para mostrar que 0 ≤ ∬ Rs e nπ x cos π x d A ≤ 1 32 onde R = 0 , 1 4 × 1 4 , 1 2 .
Repita o Exercício 15 para a integral ∬ Rs e n x + y d A 15 ) Utilize uma calculadora programável ou computador (ou o comando de soma de um SCA) para estimar ∬ R1 + x e - y d A onde R = 0 ,1 × 0 ,1 .
Calcule a integral iterada.int_0^2 int_0^1 (2 x + y)^8 d x d y