Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.6 - Ex. 10d

Determine o volume dos sólidos W abaixo.

W é o sólido acima do plano x y limitado pelas superficies z = 0 , x + y + z = 1 e x 2 + y 2 = 1 .

Passo 1

Bom galera, vamos começar identificando as superfícies formadas pelas equações que a questão nos deu:

z = 0 → P l a n o

x + y + z = 1 →   P l a n o

x 2 + y 2 = 1 → C i l i n d r o

Onde a gente tem a equação que podemos isolar o z pra fica em função de x e y :

z = f x , y = 1 - x - y

Passo 2

Belezinha, pra mudar de variavel temos a formulinha:

∫ ∫ D f x , y d x d y

= ∫ ∫ Q g r , θ ∂ x , y ∂ r , θ   d r d θ

Onde temos que:

r 2 = x 2 + y 2

x = r cos ⁡ θ

y = r sin ⁡ θ

Passo 3

Agora, encontramos a nossa função na nova variável:

f x , y = 1 - x - y

Nas novas variáveis fica:

→ g r , θ = 1 - r cos ⁡ θ - r sin ⁡ θ

→ g r , θ = 1 - r cos ⁡ θ - sin ⁡ θ

E pra facilitar vamos dividir a nossa região D em duas partes, bem assim:

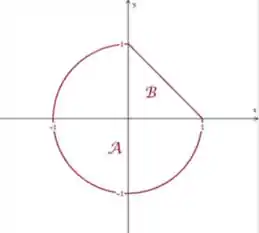
Temos:

A → x 2 + y 2 = 1

B → y = 1 - x

Assim, na nova váriavel temos a região:

A :

0 ≤ r ≤ 1

π 2 ≤ θ ≤ 2 π

E a região B na variavel original é:

y = 1 - x

0 ≤ y ≤ 1 - x

0 ≤ x ≤ 1

Passo 4

Show de bolinhas, a gente precisa calcular o determinante jacobiano, que pode ser calculado simplismente assim, com o determinante de uma matriz formada pelas derivadas parciais:

∂ x , y ∂ r , θ = det ⁡ ∂ x ∂ r ∂ x ∂ θ ∂ y ∂ r ∂ y ∂ θ

Então, colocamos os valores:

det ⁡ cos ⁡ θ - r sin ⁡ θ sin ⁡ θ r cos ⁡ θ = r

Passo 5

Por fim, montamos as integrais e calculamos:

A = ∫ ∫ Q g r , θ ∂ x , y ∂ r , θ   d r d θ

→ A = ∫ π 2 2 π ∫ 0 1 1 - r cos ⁡ θ - sin ⁡ θ r   d r d θ

→ A = ∫ π 2 2 π ∫ 0 1 r - r 2 cos ⁡ θ - sin ⁡ θ   d r d θ

Integramos a primeira vez:

A = ∫ π 2 2 π r 2 2 - r 3 3 cos ⁡ θ - sin ⁡ θ 0 1 d θ

= ∫ π 2 2 π 1 2 - cos ⁡ θ + sin ⁡ θ 3 d θ

E integramos denovo:

A = - cos ⁡ θ + cos 3 ⁡ θ 3 π 2 2 π

= π + 1 3 - π 4 + 1 3 = 3 π 4 + 2 3

Agora ainda temos B :

B = ∫ 0 1 ∫ 0 1 - x 1 - x - y   d y d x

Que integrando e calculando teremos:

= 1 6

E só somamos as duas regiões:

A + B = 3 π 4 + 2 3 + 1 6

= 3 π 4 + 5 6

E prontinho. 😊

Resposta

3 π 4 + 5 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dada, colocando-a em coordenadas polares. ∬ De - x 2 - y 2d A , onde D é a região delimitada pelo semicírculo x = 4 - y 2 e o eixo y .
A região dentro do círculo x - 1 2 + y 2 = 1 e fora do círculo x 2 + y 2 = 1 .
Utilize a integral dupla para determinar a área da região.A região dentro do círculo r = 1 + cos ⁡ θ e r = 3 cos ⁡ θ .
Calcule o valor da integral múltipla. ∫ ∫ D xd A Onde D é a região do primeiro quadrante que se encontra entre os círculos x 2 + y 2 = 1 e x 2 + y 2 = 2 .
Descreva a região cuja área é dada pela integral ∫ 0 π 2 ∫ 0 s e n 2 θ rd rd θ