Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 36
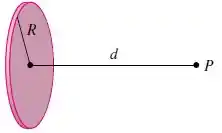
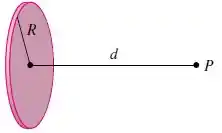
Um disco uniformemente carregado tem raio e densidade de carga superficial como na figura. O potencial elétrico no ponto a uma distância ao longo do eixo perpendicular central do disco é
Onde é uma constante (chamada constante de Coulomb). Mostre que
Para grande
Passo 1
Faaaala turma, beleza?
Nessa questão ele forneceu o potencial de um disco de raio no que está a uma distância , e esse disco possui uma densidade de carga superficial . Veja abaixo:
Onde, é uma constante (chamada constante de Coulomb).
A partir disso, devemos mostrar que o potencial para um muito grande é aproximadamente:
Para conseguirmos resolver esta questão, precisamos trabalhar com a função potencial elétrico.
Perceba que apenas essa parte da equação do potencial depende de , certo?
Onde, .
Para obter nossa resposta, vamos verificar o que acontece com o potencial quando for muito maior que , ou seja, tender ao infinito:
Como os termos não dependem de , podemos colocar em evidencia.
Seu objetivo é resolver o limite!
Feito isso, você conseguira provar que:
Vamos nessa!!
Passo 2
Queremos mostrar que para uma distância muito grande, ou seja, , temos o potencial como:
Vamos começar analisado nosso potencial. Temos que:
Repare que somente uma parte da expressão depende da distancia . Nos permitindo reescrever a equação da seguinte forma:
Onde, .
Como queremos saber o potencial para d muito grande, ou seja, d tendendo ao infinito. Teremos que aplicar um limite:
E observe que os termos não dependem de , assim podemos colocar em evidência.
Passo 3
Agora temos que resolver esse limite:
Se aplicarmos o limite direto, vamos ter:
Veja que vamos ter uma indeterminação! Precisamos então fazer uma manipulação com esta nossa função para que esta indeterminação suma.
Uma estratégia em resolução de limites, é multiplicar e dividir pela expressão com sinal positivo entre os termos, da seguinte forma:
Repare que não mudamos a forma original. Pois se dividir as expressões vai ser igual .
Fazendo a multiplicação, vamos ter:
Simplificando, obtemos:
Passo 4
Agora vamos avaliar esse limite.
Colocando o em evidência no denominador, temos:
Aqui podemos fazer a seguinte analise, separar em dois limites:
No segundo limite, quando o termo . Logo,
Assim temos:
Se avaliarmos esse limite, percebemos que ele vai tender a zero quando for para o infinito.
Além disto, podemos desconsiderar o termo porque d é muito maior que ele. Ficando com:
Podemos concluir que no infinito, ou seja, a expressão pode ser reduzida a:
Se aplicar o limite nessa expressão, com também vai ser zero.
Resposta
Demonstração.