26.
Passo 1
Neste exercício, vamos calcular a integral abaixo, usando método da substituição:
Fazendo – se
Teremos:
No final do livro, em Tabelas de integrais, temos:
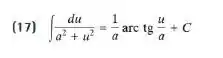
Portanto,
26.
Neste exercício, vamos calcular a integral abaixo, usando método da substituição:
Fazendo – se
Teremos:
No final do livro, em Tabelas de integrais, temos:
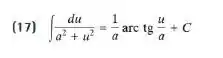
Portanto,