Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.4 - Ex. 1c
Dê os domínios e esboce os gráficos de e
e
Passo 1
Para achar basta somar as duas fuções:
Como não existe raiz quadrada de números negativos:
Então o domínio é:
E seu grafico é dado por:
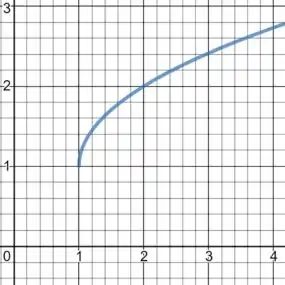
Passo 2
Para achar basta dividir as duas fuções:
Neste caso a raiz não pode ter números negativos. Então seu domínio é:
E seu grafico é dado por:
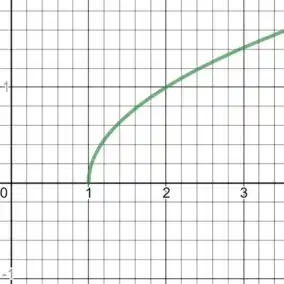
Resposta
e
Exercícios de Livros Relacionados
Sejam f x = x e g x = x 3 + 1 . Determine:(a) f ( g 2 ) (b) g ( f 4 ) (c) f ( f 16 ) (d)g ( g 0 ) (e) f ( 2 + h ) (f) g ( 3 + h )
Seja g x = x . Encontre:(a) g 5 s + 2 (b) g ( x + 2 ) (c) 3 g ( 5 x ) (d) 1 g x (e) g ( g ( x ) ) (f) g x 2 - g ( x 2 ) (g) g 1 x (h) g x - 1 2 (i) g ( x + h )
Determine as fórmulas para f ∘ g e g ∘ f e estabeleça os domínios das compostas. f x = x 2 g x = 1 - x
Determine as fórmulas para f ∘ g e g ∘ f e estabeleça os domínios das compostas. f x = x - 3 g x = x 2 + 3
Determine as fórmulas para f ∘ g e g ∘ f e estabeleça os domínios das compostas. f x = 1 + x 1 - x g x = x 1 - x