Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.12 - Ex. 13
Encontrar as derivadas das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico.
Passo 1
Beleza, aqui a gente vai usar a Regra do Quociente pra derivar.
Fica assim:
Prontinho! Encontramos a derivada! 😄
Passo 2
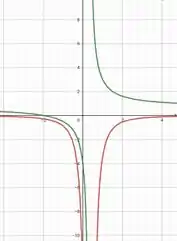
Nem precisa comparar com software né galera, mas já que pediram...
E a gente pode ver no gráfico também, aqui tá a função em verde e a derivada em vermelho:
Resposta
Exercícios de Livros Relacionados
De acordo com a Lei de Kepler, os planetas no nosso sistema solar movem-se em órbitas elípticas em torno do Sol. Se a posição do planeta mais próximo do Sol ocorrer no instante t = 0 , então a distânc
Usando as fórmulas do Exercício 72 , encontre a distância de Marte ao Sol quando t = 1 ano. Para Marte, use a = 228 × 10 6 km, e = 0,0934 e T = 1,88 ano.
76-77 Verifique o resultado do Exercício 75 para f ( x ) .77- f x = 3 x - 1 3
78-81 Use o resultado do Exercício 75 para calcular a derivada da função f( x ) dada.80- f x = x x + 1
76-77.Verifique o resultado do Exercício 75 para f x . 76. f x = 2 x + 3 2