Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 29
Encontre a área da região que está dentro de ambas as curvas
Passo 1
Vamos plotar as curvas para termos ideia da área que a gente tá calculando.
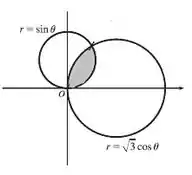
Portanto, queremos a área dessa região sombreada.
A área de uma curva em coordenadas polares é dada por
Então temos que identificar cada termo dessa integral aí, substituir e calcular. Para encontrar esse intervalo, no caso dessa questão, vamos precisar encontrar os pontos de interseção das duas curvas, já que queremos a área dentro de ambas as curvas.
Passo 2
Para que encontremos os intervalos de integração, basta igualarmos as duas curvas:
Então vamos pensar. Se a gente imaginar uma reta bem no ponto de interseção entre as duas curvas, é como se nossa região sombreada fosse a curva de até e depois passasse a ser a curva , de até .
Vê se você consegue visualizar isso:
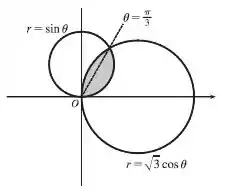
Então, teremos dois intervalos de integração:
E
Passo 3
Continuando, falta a gente descobrir quem é o .
O é a própria parametrização. Assim, como temos duas curvas, vamos ter dois (e também duas integrais, afinal, até definimos dois intervalos de integração ali no passo 2).
Então agora é só substituir e integrar esse negócio.
Passo 4
Vamos lá:
Colocando os quadrados:
Utilizando de duas identidades trigonométricas:
Essas derivadas são diretas, então a gente pode fazê-las:
Agora a gente vai aplicar os intervalos de integração:
Então colocando os intervalos:
Tomando os valores dos senos e cossenos:
Temos então que a nossa área é: