Seja o volume do sólido que está abaixo do gráfico de e acima do retângulo dado por , . Usamos as retas e para dividir em subretângulos. Sejam e as somas de Riemann calculadas utilizando como pontos amostrais os cantos inferiores esquerdos e os cantos supeirores direitos, respectivamente. Sem calcular os números , e , coloque-os em ordem crescente de valor e explique seu raciocínio.

Vamos analisar :

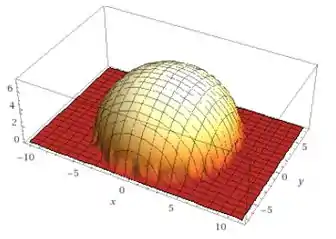
Quanto maiores os valores e que estão conectados à , menor vai seu valor final. Isso significa que para obter os maiores valores, e precisam ser o menor possível. Assim a função terá seu maior valor no canto inferior esquerdo do sub-retângulo e seu menor valor na parte superior do canto direito, e qualquer outro valor estará entre esses dois.

Como está relacionado com o inferior esquerdo e com o superior direito, o valor é maior que o valor .

Agora com , poderíamos tomar o ponto médio, vamos estimar sem cálculos que o ponto médio vai ser menor que por causa dos valores e que seriam conectados. Também podemos ver que isso vai nos dar valores ligeiramente maiores que pelo mesmo motivo. Assim, temos: