Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 10

Escreva a equação em coordenadas esféricas.

z = x 2 + y 2

Passo 1

E aii turma, beleza?? Bora lá iniciar mais uma!!!

O enunciado forneceu a expressão abaixo, e pediu para escrever em coordenadas esféricas.

z = x 2 + y 2

Primeiro vamos lembrar como é descrito coordenadas esféricas, beleza?

Ao analisar um ponto P na esfera, conseguimos extrair as seguintes expressões:

x 2 + y 2 + z 2 = ρ 2

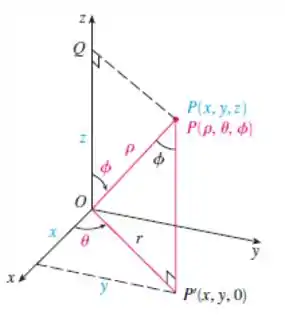
Onde,

x = ρ s e n   ϕ cos ⁡ θ

y = ρ s e n   ϕ   s e n   θ

  z = ρ cos ⁡ ϕ

Conhecendo essas relações, precisamos agora substituir na expressão dada.

Vamos nessa pessoal!!

Passo 2

Iremos analisar primeiramente a seguinte equação:

z = x 2 + y 2

Das equações de transformação para coordenadas esféricas, temos:

x = ρ s e n   ϕ cos ⁡ θ

  y = ρ s e n   ϕ   s e n   θ

  z = ρ cos ⁡ ϕ

Aplicando as equações de transformação, temos:

ρ cos ⁡ ϕ = ρ s e n   ϕ cos ⁡ θ 2 + ρ s e n   ϕ   s e n   θ 2

ρ c o s ϕ = ρ 2 s e n 2 ϕ cos 2 ⁡ θ + ρ 2 s e n 2 ϕ s e n 2 θ

ρ c o s ϕ = ρ 2 s e n 2 ϕ ( cos 2 ⁡ θ + s e n 2 θ )

Da relação fundamental da trigonometria s e n 2 x + cos 2 ⁡ x = 1 , podemos simplificar a expressãoa anterior, obtendo:

ρ c o s ϕ = ρ 2 s e n 2 ϕ

Simplificando temos que:

cos ⁡ ϕ = ρ s e n 2 ϕ

É possível ainda isolar o ρ , fazendo isso temos:

cos ⁡ ϕ s e n 2 ϕ = ρ

cos ⁡ ϕ s e n   ϕ × s e n   ϕ   = ρ

Sabemos que,

cot ⁡ x = cos ⁡ x s e n   x

csc ⁡ x = 1 s e n   x

Logo, podemos simplificar a equação para:

ρ = cot ⁡ ϕ csc ⁡ ϕ

Resposta

ρ = cot ⁡ ϕ csc ⁡ ϕ

ρ c o s ϕ = ρ 2 s e n 2 ϕ ( cos 2 ⁡ θ + s e n 2 θ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sólido delimitado abaixo pela esfera r = 2 cos f e acima pelocone z = 2x2 + y 2
Esfera e cones Encontre o volume da porção da esfera sólidar ≤ a que está entre os cones f = p/3 e f = 2p/3.
Seja D a calota menor cortada de uma esfera sólida de raio de2 unidades por um plano a uma distância de 1 unidade do centro da esfera. Expresse o volume de D como uma integral triplaiterada em coorden
Como são avaliadas integrais triplas em coordenadas cilíndricas e esféricas? Como são encontrados os limites de integra-ção? Dê exemplos.
Buraco em uma esfera Um buraco cilindrico é feito através de uma esfera sólida, o eixo do buraco sendo um diâmetro da esfera. O volume do restante do sólido é V = 2 ∫ 0 2 π   ∫ 0 3   ∫ 1 4 - z 2   r d