Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.5 - Ex. 1
Encontre a área da superfície.
A parte do plano que está acima do retângulo .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A gente precisa calcular a área de uma superfície, que é parte de um plano!
Precisamos lembrar que a área do gráfico de uma função sobre um domínio é calculada assim:
Então a gente vai definir quem é , calcular as derivadas parciais, e substituir na fórmula.
Daí, nosso problema vira descobrir quem é e calcular essa integral!
Passo 2
Bom, nossa superfície é definida pela equação:
Vamos isolar o pra termos uma função :
Então agora podemos calcular as derivadas parciais. Lembrando que quando fazemos uma derivada parcial em função de uma variável, a outra é considerada constante:
Agora em função de :
Então substituindo na nossa integral:
Resolvendo as contas:
Como é uma constante, pode sair da integral:
Só que lembra que a gente consegue calcular a área de uma região no plano , assim:
Então:
Basta a gente calcular a área do domínio que vamos ter a área da superfície!
Passo 3
Nosso domínio é um retângulo:
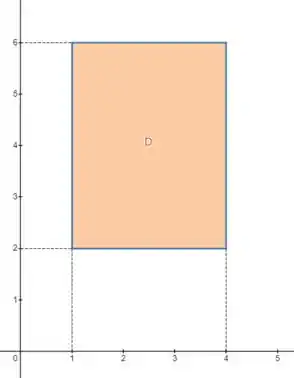
A área dessa região a gente pode calcular fazendo :
Então calculamos nossa área da superfície: