Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.2 - Ex. 68
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.
Passo 1
Fala galerinha tranquilidade, nesse dois exercícios nós teremos que compreender o que está acontecendo dentro do integrando para esboçar a região, uma dica é tentar zerar algumas variáveis e ver cada um dos pontos onde ficam.
Passo 2
Nesse caso sabemos que é algo que lembra algo circular pelo formato da função, no entanto para essa eu sugiro que se use algum tipo de programa que gera gráficos pois é um sólido complexo de se esboçar:
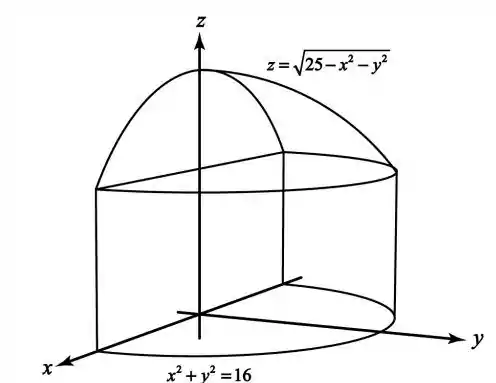
Passo 3
E a região delimitante é a parte de um semi circulo:
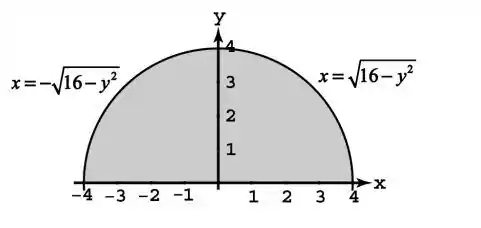
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 1 .y = x 2 ,y = 4 ,z = 0 e z = 4
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 3 .z = 1 - x 2 ,z = 0 ,x + y = 4 e y = 0
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 6 .z = x 2 + 1 ,z = 0 ,y = 0 ,x = 0 ,x = 4 e y = 5
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 10 .z = 0 ,x 2 + y 2 = 16 e z = 10 + x
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 1 1 .x 2 + y 2 - 4 x - 6 y + 4 = 0 ,z = 0 e z = 5 y