Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 40

Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ .

E é limitado pelo cilindro parabolóico z = 1 - y 2 e pelos planos x + z = 1 , x = 0 e z = 0 ;

ρ x , y , z = 4

Passo 1

Olá, desbravador dos números! Vamos explorar e solucionar essa questão de cálculo juntos. Partiu!

Primeiro, vamos entender bem o enunciado e definir a nossa estratégia de resolução.

Nosso objetivo é encontrar a massa m do sólido E e determinar o centro de massa x - , y - , z - do sólido E .

Para isso utilizaremos integrais triplas para calcular a massa e os momentos do sólido, pois a massa é dada por

m = ∭ E ρ   d V

Para encontrarmos o centro de massa precisamos encontrar antes os momentos do sólido, que são:

x - = M y z = ∭ E x   ρ   d V

y - = M x z = ∭ E y   ρ   d V

z - = M x y = ∭ E z   ρ   d V

Mas antes de começarmos precisamos definir os limites de integração para a região E .

  • O plano x = 0 e o plano x + z = 1 nos dão a variação de x :

    • 0 ≤ x ≤ 1 - z

  • O plano z = 0 e o cilindro parabólico z = 1 - y 2 nos dão a variação de z :

    • 0 ≤ z ≤ 1 - y 2

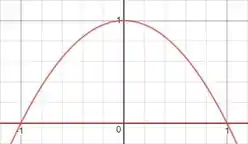
  • A variação de y é dada pelos pontos em que o cilindro parabólico cruza o eixo y , ou seja:

- 1 ≤ y ≤ 1

Passo 2

A massa m é dada por:

m = ∭ E ρ   d V = ∭ E 4   d V

Definindo os limites de integração:

m = ∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4   d x d z d y

Integrando em relação a x :

m = ∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4   d x d z d y = 4 ∫ - 1 1 ∫ 0 1 - y 2 1 - z   d z d y

Integrando em relação a z :

4 ∫ - 1 1 ∫ 0 1 - y 2 1 - z   d z d y = 4 ∫ - 1 1 z - z 2 2 0 1 - y 2 d y

Substituindo os limites de integração:

= 4 ∫ - 1 1 1 - y 2 - 1 - y 2 2 2   d y = 4 ∫ - 1 1 1 - y 2 - 1 - 2 y 2 + y 4 2   d y

= 4 ∫ - 1 1 1 2 - y 4 2   d y = 2 ∫ - 1 1 ( 1 - y 4 )   d y

Integrando em relação a y :

2 y - y 5 5 - 1 1 = 2 1 - 1 5 - - 1 + 1 5

= 2 1 - 1 5 + 1 - 1 5 = 2 2 - 2 5

m = 2 8 5 = 16 5

Então, a massa m é:

m = 16 5

Passo 3

O centro de massa é dado por ( x - , y - , z - ) onde:

x - = M y z m                     y - = M x z m                     z - = M x y m

Calculando os momentos, primeiro no plano y z

M y z = ∭ E x   ρ   d V

Definindo os limites de integração:

∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4 x   d x d z d y

Integrando em relação a x :

∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4 x   d x d z d y = ∫ - 1 1 ∫ 0 1 - y 2 2 1 - z 2 d z d y

Integrando em relação a z :

∫ - 1 1 ∫ 0 1 - y 2 2 1 - z 2 d z d y = ∫ - 1 1 - 2 1 - z 3 3 0 1 - y 2   d y

Substituindo os limites de integração:

∫ - 1 1 - 2 1 - 1 - y 2 3 3 + 2 3   d y = ∫ - 1 1 - 2 y 6 3 + 2 3   d y

Integrando em relação a y :

- 2 y 7 21 + 2 y 3 - 1 1 = 2 - 2 21 + 2 3

= 2 - 2 + 14 21 = 24 21

M y z = 8 7

No plano x z

M x z = ∭ E y   ρ   d V

Definindo os limites de integração:

∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4 y   d x d z d y

Integrando em relação a x :

∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4 y   d x d z d y = ∫ - 1 1 ∫ 0 1 - y 2 4 y 1 - z   d z d y

Integrando em relação a z :

∫ - 1 1 ∫ 0 1 - y 2 4 y 1 - z   d z d y = ∫ - 1 1 - 4 y 1 - z 2 2 0 1 - y 2 d y

Substituindo os limites de integração:

∫ - 1 1 - 4 y 1 - 1 + y 2 2 2 + 4 y 2 d y = ∫ - 1 1 - 2 y 5 + 2 y d y

Utilizando a propriedade de que uma integral de - a a a de uma função ímpar é 0

M x z = 0

E no plano x y

M x y = ∭ E z   ρ   d V

Definindo os limites de integração:

∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4 z   d x d z d y

Integrando em relação a x :

∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 1 - z 4 z   d x d z d y = ∫ - 1 1 ∫ 0 1 - y 2 4 z 1 - z   d z d y

= ∫ - 1 1 ∫ 0 1 - y 2 4 z - 4 z 2   d z d y

Integrando em relação a z :

∫ - 1 1 ∫ 0 1 - y 2 4 z - 4 z 2   d z d y = ∫ - 1 1 2 z 2 - 4 z 3 3 0 1 - y 2 d y

Substituindo os limites de integração:

∫ - 1 1 2 ( 1 - y 2 ) 2 - 4 ( 1 - y 2 ) 3 3 d y = ∫ - 1 1 2 1 - 2 y 2 + y 4 - 4 3 1 - 3 y 2 + 3 y 4 - y 6   d y

= ∫ - 1 1 2 - 4 y 2 + 2 y 4 - 4 3 + 4 y 2 - 4 y 4 + 4 3 y 6   d y = ∫ - 1 1 2 3 - 2 y 4 + 4 3 y 6   d y

Integrando em relação a y :

2 3 y - 2 y 5 5 + 4 y 7 21 - 1 1 = 2 2 3 - 2 5 + 4 21

= 2 70 - 42 + 20 105 = 2 48 105

M x y = 32 35

Passo 4

Calculando as coordenadas do centro de massa:

x - = M y z m = 8 7 16 5 = 5 14

y - = M x z m = 0 16 5 = 0

z - = M x y m = 32 35 16 5 = 2 7

Então, temos:

x - , y - , z - = 5 14 , 0 , 2 7

Resposta

m = 16 5

x - , y - , z - = 5 14 , 0 , 2 7

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular a massa e as coordenadas do centro de massa dos sólidos delimitados pelas superfícies dadas, supondo a densidade de massa constante. x 2 + y 2 + z 2 - 2 z
Determinar a massa do sólido acima do plano X Y , delimitado pelo cone 9 x 2 + z 2 = y 2 e o plano y = 9 . A densidade no ponto P ( x , y , z ) é proporcional à distância do ponto ao plano X Y .
Calcular a massa dos sólidos limitados pelas superfícies dadas, considerando a densidade de massa igual a 4 k g / m 3 . z = 4 - x 2 - y 2ez = x 2 + y 2
Verificar que o centro de massa de uma esfera de raio 1 coincide com seu centro, sabendo que a sua distribuição de massa é homogênea.
Calcular a massa e as coordenadas do centro de massa dos sólidos delimitados pelas superfícies dadas, supondo a densidade de massa constante. b )x + y = 2 , z = 2 + y e os planos coordenados.