Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.3 - Ex. 39

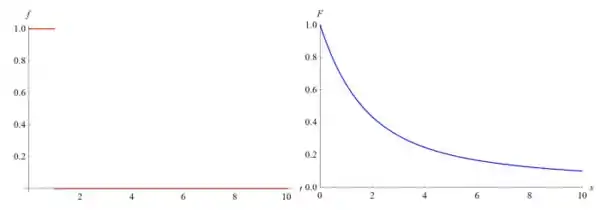
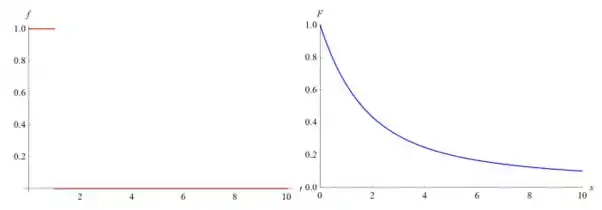
  1. Se f ( t ) = 1 - u 1 ( t ) , encontre ℒ { f ( t ) } ; compare com o Problema 30. Esboce o gráfico de y =

    2. f(t).

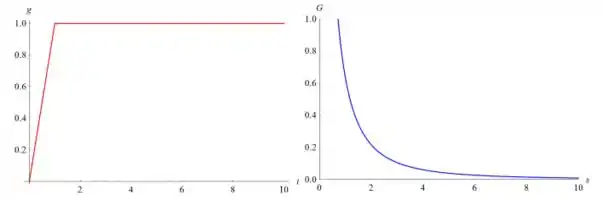
  2. Seja g ( t ) = ∫ 0 t f ( ζ ) d ζ , em que a função f está definida em (a). Esboce o gráfico de y = g(t)

    3. e encontre ℒ { g ( t ) } .

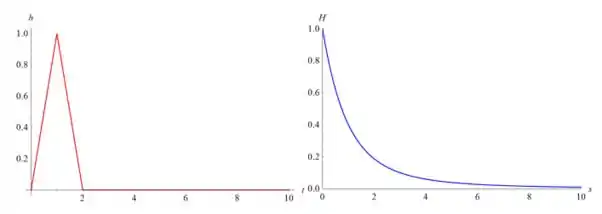
  3. Seja h ( t ) = g ( t ) - u 1 ( t ) g ( t - 1 ) , em que g está definida em (b). Esboce o gráfico de y = h(t) e

encontre ℒ { h ( t ) } .

Passo 1

Vamos começar com o geral:

A transformada de Laplace de uma função f (t) é definida como:

F ( s )   =   ℒ { f ( t ) } = ∫ 0 ∞ e - s t f ( t ) d t

Passo 2

Para a letra a, vamos lá:

Substitua a função fornecida por f (t), usando a função Heaviside H (t - 1) por u 1 ( t ) :

F ( s )   =   ∫ 0 ∞ e - s t [ 1 - H ( t - 1 ) ] d t = 1 - e ⁻ s s

Abaixo está uma comparação lado a lado de f(t) e F(s):

Passo 3

Para a letra b:

Vamos avaliar g ( t ) :

g ( t ) = ∫ 0 t f ( ξ ) d ξ = ∫ 0 t [ 1 - H ( ξ - 1 ) ] d ξ = ∫ 0 t d ξ   -   ∫ 0 t H ( ξ - 1 ) d ξ = ∫ 0 t d ξ - H ( t - 1 ) ∫ 1 t d ξ = t - ( t - 1 ) H ( t - 1 )

E agora, achamos a transformada de Laplace:

ℒ { g ( t ) } = ∫ 0 ∞ e - s t g ( t )   d t = ∫ 0 ∞ e - s t [ t - ( t - 1 ) H ( t - 1 ) ]   d t = ∫ 0 ∞ t e - s t   d t - ∫ 0 ∞ e - s t ( t - 1 ) H ( t - 1 )   d t

Resolvendo as integrais, chegamos em:

ℒ { g ( t ) } = 1 - e - s s 2

Abaixo está uma comparação lado a lado de g(t) e G(s):

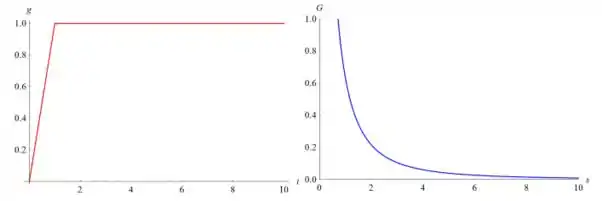
Passo 4

Na letra c:

Comece descobrindo o que h (t) é.

h ( t ) = g ( t ) - u 1 ( t ) g ( t - 1 ) = [ t - ( t - 1 ) H ( t - 1 ) ] - H ( t - 1 ) { ( t - 1 ) - [ ( t - 1 ) - 1 ] H [ ( t - 1 ) - 1 ] }

= t - 2 ( t - 1 ) H ( t - 1 ) + ( t - 2 ) H ( t - 2 )

E em seguida, ache a transformada de Laplace:

ℒ { h ( t ) } = ∫ 0 ∞ e - s t h ( t ) d t   =   ∫ 0 ∞ e - s t [ t - 2 ( t - 1 ) H ( t - 1 ) + ( t - 2 ) H ( t - 2 ) ] d t

=   - d d s ∫ 0 ∞   e - s t d t + 2 d d s ∫ 1 ∞ e - s t d t - d d s ∫ 2 ∞ e - s t d t + 2 ∫ 1 2 e - s t d t

Agora, avalie as integrais e simplifique o resultado:

h ( t )   =   - d d s ( - 1 s e - ∞   + 1 s e 0 ) + 2 d d s ( - 1 s e - ∞ + 1 s e - 1 )   - d d s ( - 1 s e - ∞ + 1 s e - 2 t ) + 2 ( - 1 s e - 2 s + 1 s e ⁻ s ) = ( 1 - e - s s ) 2

Abaixo está uma comparação lado a lado de h(t) e H(s):

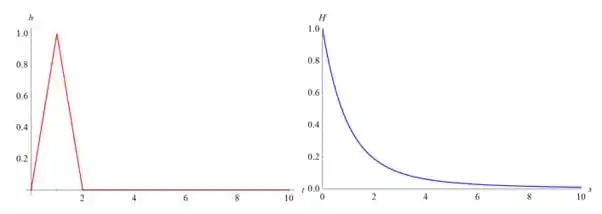
Resposta

  2. ℒ { g ( t ) } = 1 - e - s s 2

  3. h ( t )   = ( 1 - e - s s ) 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dosproblemas de 1a6, esboce o gráfico da função dada no intervalo t≥0 . g t =t - 1 u 1 t -2 t - 2 u 2 t + ( t - 3 )u 3 ( t )
Em cada um dosproblemas de 19a 24, encontre a transformada de Laplace inversa da função dada. F s = ( s - 2 ) e - s s 2 - 4 s + 3
Em cada um dosproblemas de 13a18, encontre a transformada de Laplace da função dada. f t = 0 ,t1 t 2 - 2 t + 2 , t ≥ 1
Em cada um dosproblemas de 1a6, esboce o gráfico da função dada no intervalo t≥0 . g t =f t - 3 u 3 t ,e mq u ef t = sen ⁡ t
Em cada um dosproblemas de 19a 24, encontre a transformada de Laplace inversa da função dada. F s = 2 e - 2 s s 2 - 4