Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.2 - Ex. 3
Encontre uma equação da tangente à curva no ponto correspondente ao valor do parâmetro dado.
Passo 1
Opa, tudo jóia? Questãozinha de curva paramétrica, vamos lá!
A questão nos dá uma curva definida por
E pede para encontrarmos uma reta tangente no ponto onde
Mas como fazemos isso?
De forma geral, podemos usar a seguinte fórmula
Onde o ponto será o ponto correspondente ao parâmetro , nesse caso , e é a inclinação da reta tangente!
Ok, para encontrar a gente substitui o valor de na expressão de . Da mesma forma a gente faz para encontrar o , mas e a inclinação ?
A inclinação é dada pela seguinte derivada
Então a gente só precisa encontrar nosso ponto e as derivadas e para montar nossa expressão da reta tangente!
Passo 2
Sejam as seguintes equações paramétricas
Encontrando suas respectivas derivadas, temos
E portanto será
Ou ainda
Substituindo o valor de
Passo 3
Agora vamos encontrar o ponto
Para , temos
De forma que
Prosseguindo, para , temos
De forma que
E assim
Substituindo tudo na fórmula da reta tangente, temos
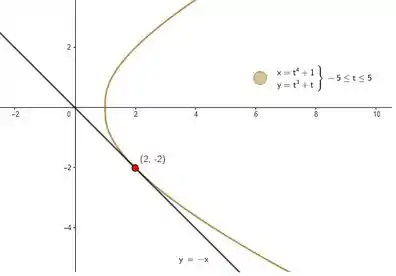
Passo 4
De brinde, se a gente plotar o gráfico da curva e da reta tangente temos o seguinte
