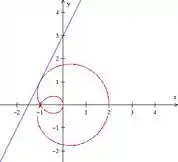
Encontre uma equação da(s) tangente(s) à curva no ponto dado. A seguir, trace a curva e a(s) tangente(s) com auxílio de uma ferramenta gráfica.
Passo 1
Oie, meu amado amigo. Tudo bem com você?
Vou te ajudar a resolver essa atividade hoje. Aqui a gente precisa encontrar a equação tangente a curva parametrizada:
No ponto:
A equação da reta tangente a uma curva em um determinado ponto genérico é dada por:
Em que:
Assim, precisamos encontrar as derivadas de e em relação a e substituir nessa fórmula.
Passo 2
Vamo começar pela derivada de :
Aqui a deriva é relativamente simplis, precisamos apenas utilizar da regra da cadeia no segundo termo:
Agora a derivada de :
Substituindo na fórmula
Passo 3
Agora a gente precisa descobrir o valor do parâmetro correspondente ao ponto de tangencia . Para isso é igualar o ponto à parametrização da curva e resolver o sistema.
Das identidades trigonométricas podemos dizer que:
Da primeira equação, tiramos que:
Assim:
Ou:
Testando esses dois valores de na segundo equação do sistema, vemos que a única que atende a é quando .
Substituindo no vetor tangente, temos:
Passo 4
Assim, a equação da reta tangente no ponto fica:
Substituindo os pontos e o valor numérico de :
Passo 5
Agora vamos traçar a curva e a nossa reta tangente no ponto .
Vamos usar a ajuda do Winplot, como a própria questão pede, pois esse tipo de curva não é nada fácil de desenhar na mão.
Mas em último caso, se estivermos no meio da floresta perdidos e sem pc, sempre podemos chutar vários valores para e ir plotando vários pontos pra ver a cara que a curva vai tomando e depois ligar os pontinhos, beleza?
Pra reta vale o mesmo raciocínio. Mas, plotar uma reta na mão é beeeeeem mais de boas e nesse caso aí é só fazer uma reta cortando o eixo em e com inclinação igual a .
Dito isso, nossa curva e nossa reta ficam:
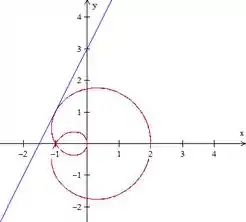
Resposta