Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 16

Encontre e esboce o domínio da função.

f x , y = x 2 + y 2 - 4

Passo 1

Oie, tudo bem? Vamos resolver essa atividade com você hoje.

Queremos determinar o domínio de f ( x , y ) , ou seja, queremos saber que valores de x e y   que podem ser usados para que f ( x , y ) seja real.

A função que nos foi dada foi a:

f x , y = x 2 + y 2 - 4

Para definir o domínio, é melhor olhar para as restrições.

Sabemos que não podemos ter raiz negativa.

Passo 2

Então devemos analisar a restrição:

x 2 + y 2 - 4 ≥ 0

Isso implica que:

x 2 + y 2 ≥ 4

Logo, o domínio é de f ( x , y ) é

{ ( x , y ) | x 2 + y 2 ≥ 4 }

note que nossa restrição é uma circunferência de raio r = 2 , esboçando o gráfico, temos:

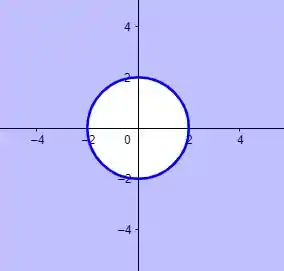
Isso é, o conjunto de valores externo a nossa circunferência, é toda a região de azul do gráfico e também a fronteira de circunferência.

Resposta

D :   { ( x , y ) | x 2 + y 2 ≥ 4 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico da função: f x , y = x 2 + y 2
Determine e esboce o domínio da função. f x , y = y + 25 - x 2 - y 2
Esboce o gráfico da função f x , y = 10 - 4 x - 5 y
Determine e esboce o domínio da função. f x , y , z = 1 - x 2 - y 2 - z 2
Dois mapas de contorno são mostrados. Uma é para uma função f cujo gráfico é um cone. A outra é para uma função t cujo gráfico é um parabolóide. Qual é qual e por quê?