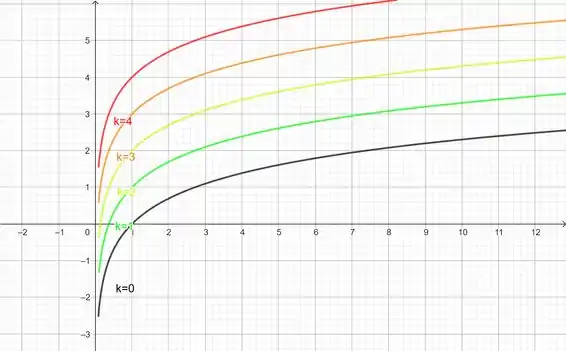
Faça o mapa de contornos da função mostrando várias curvas de nível.
Passo 1
Olá, meu querido. Vamos resolver essa atividade junto, beleza?
A gente tem a função:
E a gente quer desenhar o mapa de contornos da função.
Um diagrama de contorno, também conhecido como mapa de contorno ou gráfico de contorno, é uma representação gráfica de uma função de duas variáveis . Ele mostra curvas de nível, que são linhas que conectam pontos com o mesmo valor de . Estas curvas ajudam a visualizar a forma e a variação da função em uma superfície bidimensional.
Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível.
Basta fazer
e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.
Passo 2
Então vamos organizar:
Igualando a uma constante real :
Agora basta que a gente de diferentes valores para e gere o gráfico:
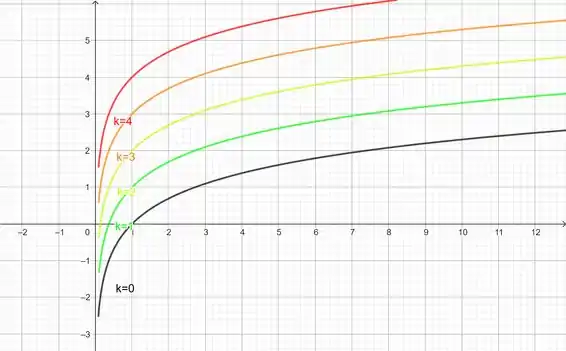
Resposta