Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 54
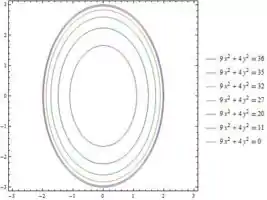
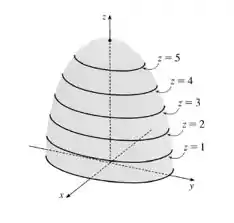
Esboce um mapa de contorno e um gráfico da função e compare-os.
Passo 1
Olá, tudo bem? Espero que você esteja bem e disposto a aprender um pouco mais hoje.
Temos que desenhar o mapa de contorno e o gráfico da função:
Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível.
Basta fazer e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.
Para se desenhar o gráfico da função, basta fazer . Trata-se de uma superfície em .
Após fazermos iremos analisar se a função que temos não é similar a alguma função que conhecemos, e com ajuda da curva de nível, iremos ‘esticar’ o comportamento que encontrarmos na curva de nível em todo o eixo .
Passo 2
Para desenhar o mapa de contorno:
Retirando a raiz:
Agora vamos colocar de forma a termos apenas em um dos lados da igualdade:
Dividindo todo mundo por :
Organizando em forma de fração:
(Para , pois senão, o denominador vai dar zero!)
Essa é a equação da elipse com eixos e .
Variando , chega-se ao seguinte mapa de contorno:
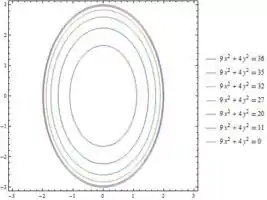
Passo 3
Para desenhar o gráfico da função:
()
Retirando o quadrado:
Agora organizando de forma a termo apenas em um dos lados da igualdade:
Essa é a equação de um elipsoide. Logo, a superfície que representa o gráfico da função é a metade superior de um elipsoide (já que ) como mostrado na figura.
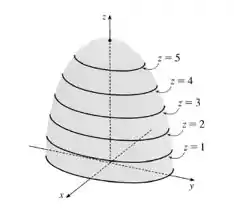
É interessante perceber que o mapa de contorno é a projeção da função no plano . E conseguimos obter um gráfico analisando o outro.
Resposta
