Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 7

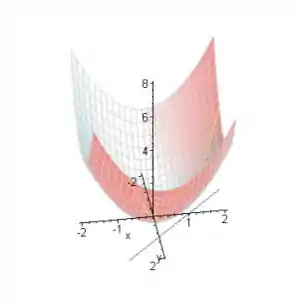
Um ponto P descreve uma curva sobre o gráfico da função f ( x ,   y )   =   x   ²   +   y   ² de modo que a sua projeção Q sobre o plano xy descreve a reta x   +   y   =   1 . Determine o ponto da curva que se encontra mais próximo do plano xy. (Desenhe a trajetóriia descrita por P.)

Passo 1

Achar a imagem a partir das informações do problema:

x + y = 1

y = 1 - x

f x , y = f x , 1 - x

f x , y = x 2 + ( 1 - x ) ²

f 5 - t , t 2 + 3 = 2 x 2 - 2 x + 1

Passo 2

Determinar os pontos críticos no intervalo:

f ( x , y ) = 2 x 2 - 2 x + 1

f ' x , y = 4 x - 2 = 0

x = 1 2

f ' ' ( x , y ) = 4 > 0

Pelo teste da derivada segunda, em x = 1 2 temos ponto de mínimo.

Passo 3

Achar o y e z:

y = 1 - x

y = 1 - 1 2

y = 1 2

z = x 2 + y ²

z = 1 2 ² + 1 2 ²

z = 1 4 + 1 4 = 1 2

Passo 4

Representar a trajetória de P:

Portanto o ponto mais próximo do plano xy é P = ( 1 2 , 1 2 , 1 2 )

Resposta

O   p o n t o   m a i s   p r ó x i m o   é   P = ( 1 2 , 1 2 , 1 2 )  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe as curvas de nível e esboce o gráfico. f x , y = 1 - x 2 - y ² ²
Desenhe as curvas de nível e esboce o gráfico. f x , y = 1 + x 2 + y ² ²
Desenhe as curvas de nível e esboce o gráfico. f x , y = 4 x 2 + y ² ²
Desenhe as curvas de nível e esboce o gráfico. f x , y = x + 3 y
Desenhe as curvas de nível e determine a imagem. f x , y = x y