Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.4 - Ex. 14
Encontre uma expressão envolvendo para uma função f cujo gráfico é uma rampa
crescente de zero em até o valor h em
Passo 1
Para o primeiro termo, a função Heaviside , definida como 1 se e 0 se , torna a função começa a aumentar em . O fator de faz com que ele atinja uma altura de h em . O segundo termo, que é ativado quando , cancela o primeiro termo.
O terceiro termo faz com que f(t) tenha um valor de h a partir de e assim por diante. f(t) também pode ser escrito como
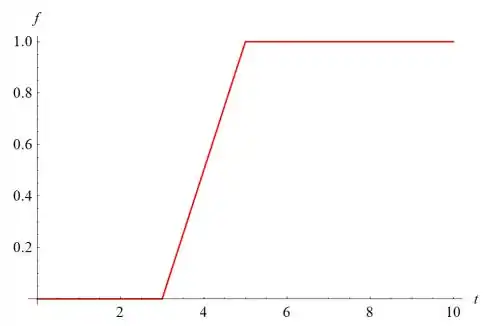
Abaixo está uma amostra de f(t) versus t se h=1, k=2 e.
Resposta
Exercícios de Livros Relacionados
Modifique o problema no Exemplo 2 desta seção substituindo o termo não homogêneo g(t) por f ( t ) = u 5 ( t ) - ( t - 5 ) - u 5 + k ( t ) ( t - 5 - k ) k Esboce o gráfico de f(t) e descreva como ele d
Considere o problema de valor inicial y ' ' + 0.1 y ' + y = f ( t ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 em que f(t) é a mesma que no Problema 19.Desenhe o gráfico da solução. Use um valor de n suficientemente
Considere o problema de valor inicial y ' ' + y = f ( t ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 em que f ( t ) = u 0 ( t ) + 2 ∑ k = 1 n ( - 1 ) k u k π ( t ) . Desenhe o gráfico de f(t) em um intervalo como 0
Considere o problema de valor inicial y ' ' + 1 3 y ' + 4 y = f k ( t ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 . em que f k ( t ) = 1 2 k ,4 - k ≤ t4 + k f k ( t ) = 0 ,0 ≤ t4 - k et ≥ 4 + k e 0 Esboce o gráfico
Considere o problema de valor inicial y ' ' + y = h ( t ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 em que h ( t ) = u 0 ( t ) + 2 ∑ k = 1 n ( - 1 ) k u 11 k / 4 ( t ) . Observe que esse problema é idêntico ao Prob