Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.6 - Ex. 5
(a) Encontre uma fórmula para a solução do problema de valor inicial e observe se ela é independente de .
(b) Use o método de Runge-Kutta com para calcular valores aproximados da solução em para diversos valores de , como
(c) Explique as diferenças, se existirem, entre a solução exata e as aproximações numéricas.
Passo 1
(a) Precisamos resolver um problema com a condição inicial Primeiro, resolva a equação homogênea correspondente , teremos que a solução é:
Agora encontre a solução específica. É da forma , uma vez que deve ser uma solução do problema inicial, substituímos pelo problema para encontrar e
A solução do ODE inicial é dada como , portanto, a solução geral é . Mas temos uma condição inicial e podemos determinar :
A solução será:
A solução não depende de .
Passo 2
(b) Usaremos Para este problema, usaremos:
Podemos ter então :
Repetimos os passos até encontrar :
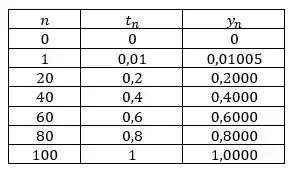
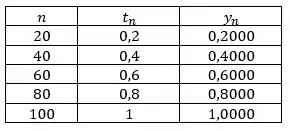
Passo 3
Para diversos valores de nós teremos:
