Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 10

(a) Encontre e identifique os cortes da superfície quádrica - x 2 - y 2 + z 2 = 1 e explique por que o gráfico parece com o gráfico do hiperboloide de duas folhas da Tabela 1 .

(b) Se a equação na parte (a) for trocada para x 2 - y 2 - z 2 = 1 , o que acontece com o gráfico? Esboce o novo gráfico.

Passo 1

(a) Pessoal, pra gente identificar os cortes de uma superfície quádrica, temos que fazer cada uma das variáveis serem iguais a uma constante, e ver o que acontece com a equação, beleza?

  • x = k :

    • - x 2 - y 2 + z 2 = 1

    - k 2 - y 2 + z 2 = 1

    z 2 - y 2 = 1 + k 2

    z 2 1 + k 2 - y 2 1 + k 2 = 1

    Isso nos daria uma hipérbole.

    Passo 2

    Bora continuar?

  • y = k :

    • - x 2 - k 2 + z 2 = 1

    z 2 - x 2 = 1 + k 2

    z 2 1 + k 2 - x 2 1 + k 2 = 1

    Novamente, uma hipérbole.

  • z = k :

- x 2 - y 2 + k 2 = 1

x 2 + y 2 = k 2 - 1

Agora temos uma elipse, mais precisamente uma circunferência, pra k 2 - 1 > 0 , ou seja:

k 2 > 1

k < - 1       o u       k > 1

Passo 2

Agora que já temos os cortes, sabemos que o gráfico vai se parecer com esse gráfico de hiperboloide de duas folhas:

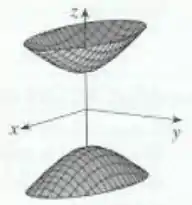
Repare que nossos cortes verticais ( x = k e y = k ) são hipérboles, e o corte horizontal ( z = k ) é uma elipse, desde que k < - 1 ou k > 1 . Ou seja, o gráfico não intercepta uma certa região de z , exatamente como no gráfico do hiperboloide de duas folhas da Tabela 1 .

Passo 3

(b) Se trocarmos a equação para x 2 - y 2 - z 2 = 1 , estamos fazendo com que o corte elíptico seja em x = k , ou seja, é como se o hiperboloide do item anterior fosse girado, de forma que seu novo eixo fosse o eixo x . Esboçando, fica assim:

Resposta

(a) x = k : h i p é r b o l e

y = k : h i p é r b o l e

z = k : e l i p s e   o u   c i r c u n f e r ê n c i a   p a r a   k < - 1   o u   k > 1

(b) O hiperboloide é girado de modo que ele tenha eixo no eixo x .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. 25 y 2 + z 2 = 100 + 4 x 2
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. 4 y = x 2 + z 2
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. 16 x 2 = y 2 + 4 z 2
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. y 2 = x 2 + z 2
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. x 2 + 4 z 2 - y = 0