Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 6
Encontre o polinômio de Taylor da função em . Trace e na mesma tela.
Passo 1
Primeiramente, para encontrar os polinômios de Taylor, precisamos saber qual a série dessa função, então vamos meter a mão na massa. Lembrando que o formato da série de Taylor é
Nos sabemos que se derivarmos a exponencial quantas vezes quisermos, continuaremos com , então o padrão para a derivada é
No cento temos que
E assim temos nosso termo geral e nossa série é
Passo 2
Para calcular , basta que achemos os primeiros termos da série e pararmos em , então
Passo 3
Traçando a função e no plano
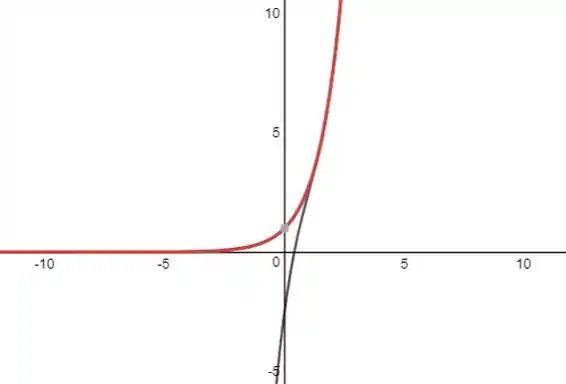
De vermelho temos a função e em cinza .
Resposta
Exercícios de Livros Relacionados
Use uma série de maclaurin na Tabela 1 para obter a série de Maclaurin da função dada. f x = x 2 l n ( 1 + x 3 )
Use a sére binomial para expandir a função como uma série de potência. Diga o raio de convergência. f x = 1 - x 4
Encontre a sére de Taylor de f(x) centrada no valor dado de a. [Suponha que f tenha expansão em uma série de potências. Não mostre que R n x → 0 .] Também encontre o raio de convergência associado. f
Encontre a sére de Maclaurin de f(x) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que R n x → 0 . ] Também encontre o raio de conve
Encontre a sére de Taylor de f(x) centrada no valor dado de a. [Suponha que f tenha expansão em uma série de potências. Não mostre que R n x → 0 .] Também encontre o raio de convergência associado. f