Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 9
Encontre o polinômio de Taylor da função em . Trace e na mesma tela.
Passo 1
Para encontrar essa série, vamos usar o método de multiplicação de séries, com as séries centradas em
Multiplicando as séries
Se analisarmos bem, teremos termos com todos os graus a partir do , e para encontrarmos , precisamos do polinômio de grau , então utilizaremos apenas os termos que tem grau ou inferior.
Passo 2
Vamos a multiplicação
Então nosso é
Passo 3
Traçando a função e no plano
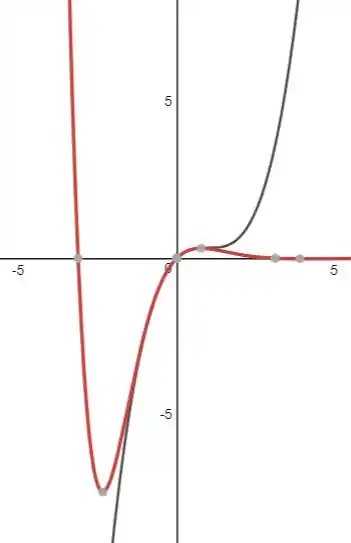
De vermelho temos a função e em cinza .
Resposta
Exercícios de Livros Relacionados
Use séries para aproximar a integral definida com a precisão indicada.
Use multiplicação ou divisão de séries de potência para encontrar os três primeiros termos não nulos na série de Maclaurin para cada função.
Encontre a soma das séries.
Use multiplicação ou divisão de séries de potência para encontrar os três primeiros termos não nulos na série de Maclaurin para cada função.
Use séries para avaliar o limite.