Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 12
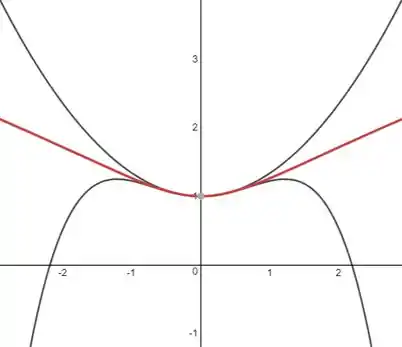
Use um sistema de computação algébrica para encontrar os polinômios de Taylor centrados em para Então, trace esses polinômios e na mesma tela.
Passo 1
Utilizando um software matemático, temos que os polinômios de Taylor para a função dada são
Os termos ímpares são então a soma dos termos com impar é igual a soma do anterior.
Passo 2
No gráfico
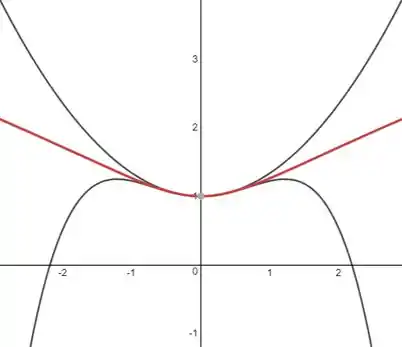
Em vermelho a função e em cinza os polinômios de Taylor.
Resposta
Exercícios de Livros Relacionados
Use as séries de Maclaurin da Tabela 1 para obter a série de Maclaurin para a função dada.
Encontre a série de Maclaurin de f (através de qualquer método) e o seu raio de convergência. Faça o gráfico de f e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a
Encontre a série de Maclaurin de f (através de qualquer método) e o seu raio de convergência. Faça o gráfico de f e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a
Encontre a soma das séries.
Encontre a soma das séries.