Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.11 - Ex. 4
Encontre o polinômio de Taylor da função centradas no número . Faça o gráfico de e na mesma tela.
Passo 1
A série de Taylor é dada por:
Os polinômios então são dados pela linearização da função (palavra complicada né?), que é assim:
Se aplicarmos a função até (porque tá pedindo ), a gente vai, no caso, derivando a função e aplicando o valor de pra achar .
Aí depois a gente aplica na série e acha o polinômio...
Passo 2
Vamos montar uma tabelinha pra ficar mais organizado...
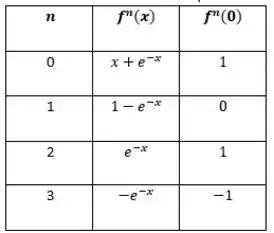
Passo 3
Agora é só jogar esses valores na série para acharmos o polinômio...
Esse é o polinômio , vamos esboçar os gráficos agora...
Passo 4
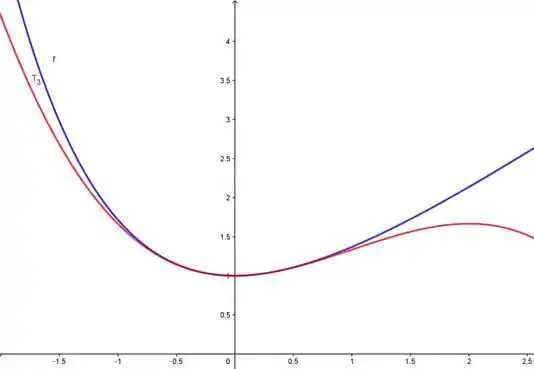
E... fim🙏
Resposta
Exercícios de Livros Relacionados
Suponha que f ( x ) tenha derivadas até ordem n em x = a . Mostre que o polinômio de Taylor de ordem =n e suas n primeiras derivadas têm os mesmos valores que f e suas n primeiras derivadas têm em x =
Encontre a série de Maclaurin para as funções nos Exercícios 11-22.21. x 4 - 2 x 3 - 5 x + 4
Propriedades de aproximação dos polinômios de Taylor - Suponha que f ( x ) seja derivável em um intervalo centrado em x = a e que g x = b 0 + b 1 x - a + … + b n x - a n seja umpolinômio de grau n com
Nos Exercícios 1-10, encontre os polinômios de Taylor de ordens 0, 1, 2 e 3 gerados por f em a.8. f x = tg x ,a = π 4
Encontre a série de Maclaurin para as funções nos Exercícios 11-22.18. 5 cos π x