Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.12 - Ex. 10

Encontre o polinômio de Taylor T n x para a função f em a . Plote f e T n na mesma tela.

f x = 3 + x 2 ,     a = 1 ,     n = 2

Passo 1

Bom, vamos começar relembrando o que é um polinômio de Taylor. Ele consiste em nada mais e nada menos que um polinômio obtido através do truncamento da série de Taylor. Logo,

T n x = ∑ i = 0 n f i a i !   x - a i

Como a questão nos disse que a = 1 e n = 2 , o nosso polinômio será:

T 2 x = f 0 1 0 ! x - 1 0 + f 1 1 1 ! x - 1 1 + f 2 1 2 ! x - 1 2

Temos agora que descobrir quem são essas derivadas da nossa função!

Passo 2

Como já montamos a função T 2 x , só nos faltou descobrir as derivadas da nossa função aplicada no ponto a = 1 . Sendo assim, vamos calcular estas derivadas!

f x = 3 + x 2 ⟹ f 1 = 2

f ' x = x 3 + x 2 ⟹ f ' 1 = 1 2

f ' ' x = 1 ⋅ 3 + x 2 - x 2 3 + x 2 3 + x 2 ⟹ f ' ' 1 = 2 - 1 2 4 = 3 8

Portanto, o nosso polinômio é:

T 2 x = 2 1 x - 1 0 + 1 2 1 x - 1 1 + 3 8 2 x - 1 2

T 2 x = 2 + 1 2 x - 1 1 + 3 16 x - 1 2

E é isso ai!

Passo 3

Agora que obtivemos o nosso polinômio de Taylor, vamos fazer seu plot e comparar com a função original. Utilizando softwares para nos auxiliar, temos:

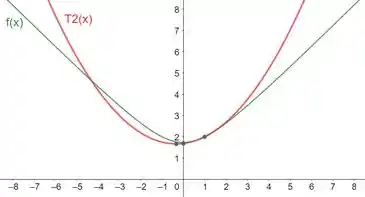
Resposta

T 2 x = 2 + 1 2 x - 1 1 + 3 16 x - 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 15-18, utilize séries para estimar os valores das integrais com um erro de magnitude menor que 1 0 - 3 . (A seção de respostas apresenta os valores das integrais arredondados para cinco
Mostre que a série de Taylor para f ( x )=t g - 1x diverge para | x |1 .
Obtenha a série de Taylor para 1 / ( 1+x ) 2 a partir da série para - 1 / ( 1 + x ) .
Nos Exercícios 41-52, utilize a Tabela 10.1 para encontrar a soma de cada uma das séries.45. π 3 - π 3 3 3⋅3 ! + π 5 3 5⋅5 ! - π 7 3 7⋅7 !+⋅ ⋅ ⋅
De acordo com o teorema da estimativa de séries alternadas, quantos termos da série de Taylor para t g- 11 teriam de ser adicionados para se ter certeza de encontrar π / 4 com um erro de magnitude men