Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 2
(a) Encontre os polinômios de Taylor até o grau 3 de centrados em . Trace e esses polinômios na mesma tela.
(b) Calcule e esses polinômios em e .
(c) Comente como os polinômios de Taylor convergem para .
Passo 1
Fala, pessoal! Tudo show?
A questão, no item (a) nos pede pra encontrar os polinômios de Taylor da função , centrados em , até o grau , ou seja, devemos fazer três integrais.
Logo, no item (b), iremos substituir e em e nos polinômios.
Já no item (c), explicar como os polinômios de Taylor convergem para .
Beleza? Vamos fazer a mágica acontecer!
Passo 2
- Primeiramente, para encontrar os polinômios de Taylor, precisamos saber qual a série dessa função, então vamos meter a mão na massa. Lembrando que o formato da série de Taylor é
- Agora iremos substituir nossa função e nossos polinômios de Taylor por , e . Show?
- Nessa função, podemos perceber, conforme o gráfico e a tabela de valores, que o polinômio de Taylor de grau superior converge para em um intervalo mais amplo em comparação com o polinômio de grau inferior.
Para isso vamos derivar algumas vezes e substituir em que é nosso centro
Expandindo a fórmula de Taylor e substituindo, teremos
Como queremos até o grau 3, então
Obs, hein? e .
Plotando nosso gráfico, teremos
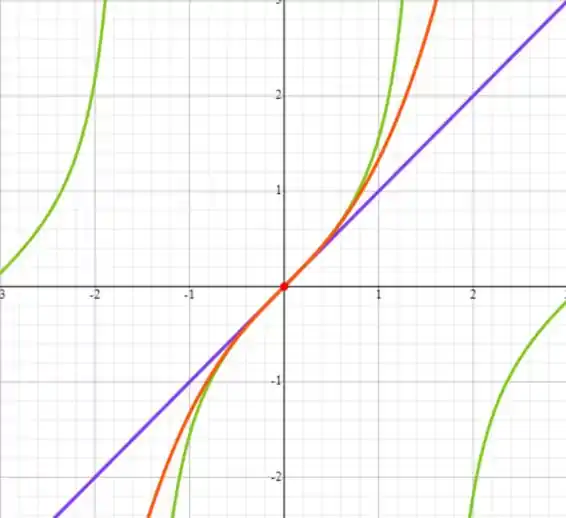
Onde, em verde, teremos , em roxo teremos e em vermelho .
Passo 3
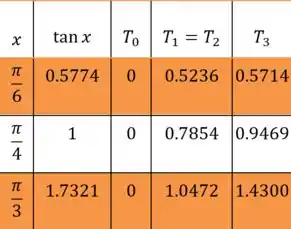
Usando uma calculadora, chegaremos a esses resultados expressos na tabela abaixo:
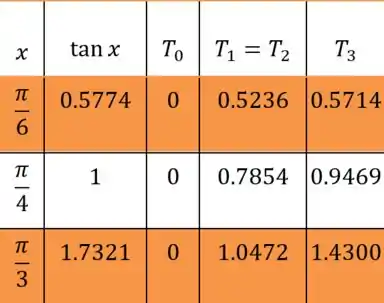
Passo 4
Podemos ver também pelos gráficos que quanto maior a distância, menor a precisão.
Resposta
-
- O polinômio de Taylor de grau superior converge para em um intervalo mais amplo em comparação com o polinômio de grau inferior.