Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 1

  1. Encontre os polinômios de Taylor até o grau 5 de f x = sen ⁡ x centrados em a = 0 . Trace f e esses polinômios na mesma tela.
  2. Calcule f e esses polinômios em x = π / 4 ,   π / 2 e π .
  3. Comente como os polinômios de Taylor convergem para f ( x ) .

Passo 1

Fala, gente bonita! Tudo belezinha?

A questão, no item (a), nos pede pra encontrar os polinômios de Taylor da função

f x = s e n   x

centrados em a = 0 , até o grau 5 , ou seja, devemos fazer cinco integrais.

Logo, no item (b), iremos substituir x = π / 4 ,     π / 2   e π em f e nos polinômios.

Já no item (c), explicar como os polinômios de Taylor convergem para f ( x ) .

Vamos mergulhar de cabeça nessa questão e fazer a mágica acontecer!

Passo 2

No item (a), para encontrar os polinômios de Taylor, precisamos saber qual a série dessa função, então vamos meter a mão na massa. Lembrando que o formato da série de Taylor é

∑ n = 0 ∞ f n ( a ) n ! x - a n

Para isso vamos derivar cinco vezes, como pede o enunciado, e substituir em x = 0 , que é nosso centro

f = s e n   x ⇒ f 0 = 0

Para a primeira derivada, e substituindo x = 0 , teremos

f ' = cos ��� x ⇒ f ' ( 0 ) = 1

Para a segunda derivada, e colocando x = 0 , chegaremos a

f ' ' = - s e n   x ⇒ f ' ' 0 = 0

Para a terceira derivada...

f ' ' ' = - cos ⁡ x ⇒ f ' ' ' 0 = - 1

Resolvendo e substituindo a quarta derivada

f 4 = s e n   x   ⇒ f 4 = 0

Por fim a quinta derivada...

f 5 = c o s   x   ⇒ f 5 = 1

Expandindo a fórmula de Taylor e substituindo, teremos

f x = f a + f ' a 1 ! x - a + f ' ' a 2 ! x - a 2 + f ' ' ' a 3 ! x - a 3 + …

Substituindo todas as informações que descobrimos, teremos

f x = s e n 0 + c o s 0 1 ! x - 0 + - s e n 0 2 ! x - 0 2 + - c o s 0 3 ! x - 0 3 + s e n 0 4 ! x - 0 4 + cos ⁡ 0 5 ! x - 0 5

Organizando a fórmula acima, chegaremos a

T 5 = x - 1 6 x 3 + 1 120 x 5

Passo 3

Lembrando que os polinômios de Taylor descobertos acima

T 0 = 0

T 1 = T 2 = x

T 3 = T 4 = x - 1 6 x 3

T 5 = x - 1 6 x 3 + 1 120 x 5

Quando jogarmos no software, como o Geogebra, teremos esse gráfico a seguir

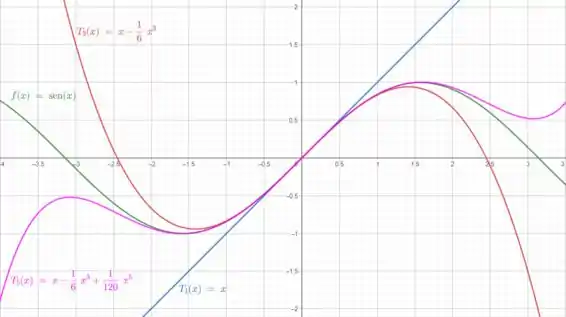
Passo 4

No nosso item (b), vamos fazer várias substituições, beleza?

Montando uma tabela para todos os resultados, teremos

Na primeira coluna, estão os valores que o enunciado nos deu para substituir por s e n   x e pelos polinômios de Taylor

T 1 = x

T 3 = x - 1 6 x 3

T 5 = x - 1 6 x 3 + 1 120 x 5

Passo 5

Agora, no item (c), podemos perceber nos cálculos do item anterior e pelo gráfico que polinômios de Taylor de grau superior, como T 5 , convergem para f em intervalos mais amplos em comparação com os polinômios de grau inferior.

Resposta

  1. T 5 = x - 1 6 x 3 + 1 120 x 5

  3. Os polinômios de Taylor de grau superior, como T 5 , convergem para f em intervalos mais amplos em comparação com os polinômios de grau inferior
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a série de Maclaurin de f (através de qualquer método) e o seu raio de convergência. Faça o gráfico de f e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a
Encontre a série de Maclaurin de f (através de qualquer método) e o seu raio de convergência. Faça o gráfico de f e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a
Prove que a série obtida no exercício 18 representa cosh ⁡ x para qualquer x .
Use a série binomial para expandir a função como uma série de potência. Espeficique o raio de convergência.
Use a série de Maclaurin para cos ⁡ x para computar o valor de cos ⁡ 5 ° com precisão de 5 casas decimais.