Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.5 - Ex. 11

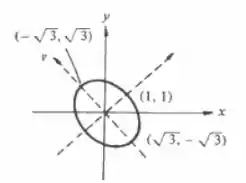
Encontre os pontos da elipse x 2 + x y + y 2 = 3 (de centro na origem) mais próximos e mais afastados da origem. Desenhe a elipse.

Passo 1

Um enunciado mais claro para este problema seria: “Determine a menor e maior distâncias de um ponto até a origem, sendo que este ponto deve estar sobre a elipse dada”. Aí pronto! Matamos o enunciado!

Lembrando que a distância de um ponto x , y à origem é dada por x 2 + y 2 , em temos de nomenclatura, neste exercício identificamos:

f = x 2 + y 2

g = x 2 + x y + y 2 - 3  

Lembrando que a f sempre vai ser a função que queremos minimizar/maximizar e g sempre representará uma restrição na forma g = 0 (no caso, o ponto DEVE estar SOBRE a elipse).

Hmmmm, mas note que termos definido f = x 2 + y 2 nos quebra as pernas, pois desse jeito teremos que derivar uma raiz quadrada e carregar ela pra sempre. Por que não definimos, melhor f = x 2 + y 2 ? Afinal, procurar o menor x 2 + y 2 é o mesmo que procurar o menor x 2 + y 2 ! Espertezaaaa!

Agora, devemos resolver o sisteminha

∇ f = λ ∇ g g = 0

Para achar os pontos de máximo/mínimo.

Passo 2

Vamos começar calculando o vetor ∇ f :

∇ f = ∂ f ∂ x , ∂ f ∂ y = 2 x , 2 y

Ótimo! Agora façamos o mesmo para o vetor ∇ g :

∇ g = ∂ g ∂ x , ∂ g ∂ y = 2 x + y , x + 2 y

E pronto, já temos os gradientes!

Passo 3

Agora, vamos substituir ∇ f e ∇ g no sisteminha ∇ f = λ ∇ g g = 0 , o que nos fornece:

2 x , 2 y = λ 2 x + y , x + 2 y x 2 + x y + y 2 - 3 = 0

Lembra-se que este sisteminha na verdade representa 3 equações:

2 x = λ 2 x + y 2 y = λ x + 2 y x 2 + x y + y 2 - 3 = 0

Agora, para resolver, o mais sensato é isolar x e y nas duas primeiras equações:

2 x 1 - λ = λ y 2 y 1 - λ = λ x

Dividindo uma equação pela outra, obtemos que x y = y x , ou seja x 2 = y 2 . Ou seja, x = ± y .

Agora, substituindo y = x na última equação do sisteminha anterior, ficamos com

x 2 + x 2 + x 2 - 3 = 0

Logo, x = ± 1 . E também, y = ± 1 .

Mas, agora tomando y = - x , ficamos com

x 2 - x 2 + x 2 - 3 = 0

Cuja solução é x = ± 3 e também, y = ∓ 3 .

Ou seja, os pontos extremos que obtivemos foram um total de 4: ( 1,1 ) , - 1 , - 1 , ( 3 , - 3 ) , - 3 , 3 . Qual deles é máximo e qual mínimo? Vamos descobrir já já.

Passo 4

Agora que temos os pontos de interesse, vamos analisar o comportamento da f nos pontos e ver o que que dá.

Primeiramente, no ponto ( ± 1 , ± 1 ) , temos:

f = x 2 + y 2 = 1 2 + 1 2 = 2

Mas, no ponto ( ± 3 , ∓ 3 ) , temos:

f = x 2 + y 2 = 3 2 + 3 2 = 6

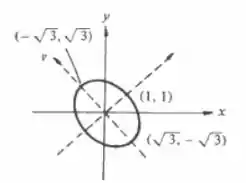
Logo, os pontos ( ± 3 , ∓ 3 ) correspondem ao máximo e ( ± 1 , ± 1 ) , correspondem ao mínimo da f !

Podemos ver este comportamento através do gráfico aproximado da elipse. Perceba como realmente esses pontos tem a distância máxima e mínima à origem.

Resposta

Máximo em ( ± 3 , ∓ 3 ) e mínimo em ( ± 1 , ± 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o ponto da curva x 2 - 2 x y + y 2 - 2 x - 2 y + 1 = 0 mais próximo da origem.
Determine, dentre os paralelepípedos-retângulos de mesmo volume, o de área máxima.
Maximize f x , y , z = x + 2 y + 3 z sujeita às restrições x 2 + y 2 + z 2 = 4 e x + y + z = 1 .
Determine a superfície de nível da função f x , y , z = x 2 + y 2 + 2 z 2 que seja tangente ao plano x + 2 y + 3 z = 4 . Qual o ponto de tangência?
Deseja-se construir um paralelepípedo-retângulo com área total de 100 c m 2 . Determirar as dimensões da caixa para o volume ser máximo.