Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.9 - Ex. 21
Encontre uma representação em série de potências para , trace e várias somas parciais na mesma tela. O que acontece quando aumenta?
Passo 1
Olá pessoal, tudo bem?
Vamos resolver este problema passo a passo.
Primeiro, nosso objetivo é encontrar uma representação em série de potências para a função . A estratégia que vamos adotar é manipular a expressão para que ela se
assemelhe à série de potências , que é uma das mais conhecidas.
Vamos começar manipulando a expressão para que se assemelhe a . Essa série de potências é conhecida e derivada da série geométrica. Sua representação é dada por:
Passo 2
Agora, vamos encontrar uma forma de manipular para que se pareça com .
Passo 3
Show! Agora vamos traçar e as primeiras somas parciais a partir da série de potências encontrada no passo anterior.
As somas parciais são aproximadas da função , calculadas usando um número finito de termos da série. À medida que adicionamos mais termos à série, as somas parciais se aproximam cada vez mais da função , especialmente dentro do intervalo de convergência da série.
Vamos plotar e as primeiras somas parciais , , no mesmo gráfico:
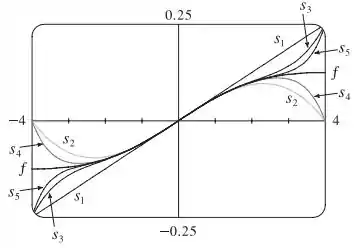
Perceba que, à medida que aumenta, as somas parciais se aproximam cada vez mais de no intervalo de convergência, ou seja, quando .
Então,