Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 34
Use a série binomial para expandir a função como uma série de potência. Especifique o raio de convergência.
Passo 1
Fala meus queridos! Vamos gabaritar essa questão!?
Vamos entender o enunciado. O objetivo é o seguinte, a partir da série binomial expandir a função fornecida como um serie de potência, e também apresentar o raio de convergência dessa série.
Como vamos resolver? Primeiro precisamos apresentar o que é a série binomial, certo? Aí sim, podemos começar a escrever a função em serie.
Essa é a representação da série de potência, a ideia é escrevermos a função dada nesse formato.
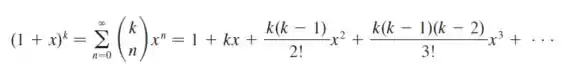
Já para obtermos o raio de convergência, precisamos avaliar a convergência da série, através da relação:
Por exemplo, para a função qualquer abaixo:
O raio para esse exemplo será:
Passo 2
Agora sim, podemos reescrever a função através da série binomial como:
E agora? Vamos expandir o somatório da série um pouco, fazendo
Repare que apenas introduzimos os valores de n e k:
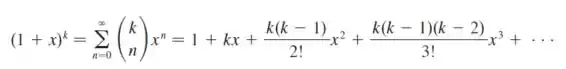
Simplificando um pouco a equação, temos:
E agora? Precisamos simplificar e escrever como série de potência. Vamos reparar os termos que se repetem e ver se conseguimos escrever em função de um somatório.
Você concordar que podemos fazer isso, manter os dois primeiros termos da série e os demais escrever como um somatório:
Passo 3
Pela análise de convergência é possível verificar que:
Sendo assim, o raio de convergência é: