Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.10 - Ex. 36
Encontre a série de Maclaurin (por qualquer método), e seu raio de convergência. Plote e seus primeiros polinômios na mesma tela. O que você observa sobre a relação entre esses polinômios e ?
Passo 1
Vamos utilizar a definição de uma série de Maclaurin para obter a série da nossa função . Logo, a série de Maclaurin da função é dada por:
Cabe a nós agora obtermos as derivadas da função , aplica-las no ponto e tentar identificar o padrão delas! Vamos começar a derivar a nossa função então.
Se continuarmos fazendo estas derivadas, vamos observar que a derivada de ordem aplicada em pode ser expressar por:
Portanto, a função é escrita através da série de Maclaurin por:
Passo 2
Para determinarmos o raio de convergência, vamos utilizar o teste da razão. Portanto,
Calculando o limite quando , temos
Portanto, o raio de convergência não depende do valor de . Desta forma, ele é dito infinito, isto é, .
Passo 3
Só nos falta obter o plot da nossa função e das primeiras aproximações. Para isto, vamos utilizar softwares que nos ajudem no esboço!
Vejamos abaixo as primeiras aproximações.
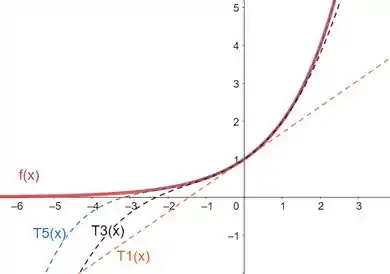
Pode-se observar que à medida em que aumentamos a ordem do polinômio, a função se aproxima cada vez mais da curva .
Resposta
Raio de convergência igual a .
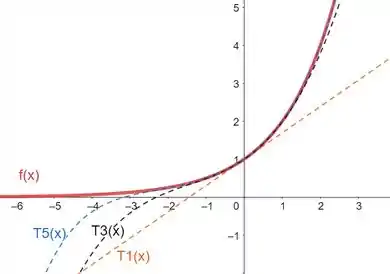
À medida em que aumentamos a ordem do polinômio, a função se aproxima cada vez mais da curva .