Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 11.10 - Ex. 42
Encontre a série de Maclaurin de (por qualquer método) e seu raio de convergência. Trace e seus primeiros polinômios de Taylor na mesma tela. O que você observa sobre a relação entre esses polinômios e ?
Passo 1
Fala pessoal, tudo bem com vocês? Bora lá resolver essa questão!
Vamos analisar o enunciado e compreender o que devemos fazer. Primeiro devemos encontrar a série de Maclaurin de e seu respectivo raio de convergência. Traçar os gráficos dos primeiros polinômios de Taylor e , e observar qual a relação entre eles.
Como resolvemos? Primeiro precisamos encontrar a série de Maclaurin a partir de algum método, podemos derivar a função e tentar comparar com alguma serie conhecida. Para determinar o raio de convergência, podemos aplicar algum teste conhecido, como o teste da razão.
Derivando a função
Agora, podemos pensar um pouco! Vê se você concorda com o raciocínio a seguir:
Lembra da série geométrica?
Onde, essa soma infinita pode ser descrita como:
Agora, compare com a nossa expressão de , concorda que ?
Assim podemos reescrever , ficando
Reorganizando os termos, temos
Passo 2
Temos uma expressão para , e agora? Como encontramos ?
Podemos integrar em ambos os lados da igualdade. Lembrando, que tudo que não depende de x podemos colocar para fora da integral
Ficando assim
Como é uma integral indefinida, irá aparecer uma constante
Para encontrar o valor de , vamos substituir na função primeiro
Agora, aplicando na função encontrada temos
Logo, temos que
Podemos ainda colocar em evidência no denominador e cancelar com o de fora
Assim nossa série fica:
Passo 3
Para determinarmos o raio de convergência de , podemos aplicar o teste da razão.
Onde nesse teste temos:
Sabendo disso, temos
Vamos reorganizar o termo dentro do módulo primeiro:
Agora, podemos voltar ao limite
Tirando do módulo
Isolando o termo que não depende do limite e resolvendo, temos
Para convergir, precisamos que
Assim, o raio é
Passo 4
O enunciado pede para traçarmos e os primeiros polinômios de Taylor () que são nada mais que você pegar a série somente até um certo termo, então os primeiros polinômios são (para )
E assim poderíamos continuar até onde quisermos.
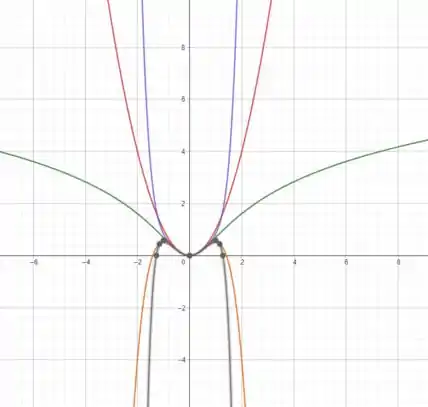
Passo 5
Traçando e os primeiros polinômios de Taylor, podemos observar que quanto maior o polinômio que pegamos (maior em ), maior a precisão em um raio maior.
