Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.5 - Ex. 11

  1. Encontre a solução do problema de valor inicial dado.
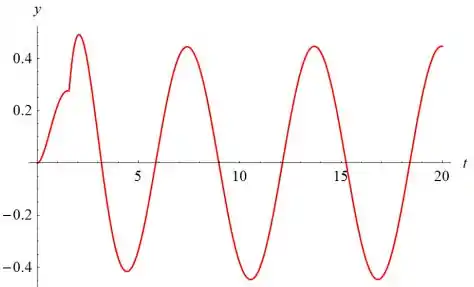
  2. Desenhe um gráfico da solução.

y ' ' + 2 y ' + 2 y = c o s   t   + δ ( t - π / 2 ) ;   y ( 0 ) = 0 ,   y ' ( 0 ) = 0

Passo 1

Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:

Y ( s )   =   ℒ { y ( t ) } = ∫ 0 ∞ e - s t y ( t )   d t

Consequentemente, a primeira e a segunda derivadas se transformam da seguinte maneira.

ℒ { d y d t } = s Y ( s )   -   y ( 0 )

ℒ { d ² y d t ² } = s ² Y ( s )   -   s y ( 0 ) - y ' ( 0 )

Aplique a conversão Laplace nos dois lados da EDO:

ℒ { y ' ' + 2 y ' + 2 y } = ℒ { c o s ( t ) + δ ( t - π / 2 ) }

ℒ { y ' ' } + ℒ { 2 y ' } + ℒ { 2 y } = ℒ { c o s ( t ) } + ℒ { δ ( t - π / 2 ) }

s ² Y ( s ) - s y ( 0 ) - y ' ( 0 ) + 2 s Y ( s ) - y ( 0 ) + 2 Y ( s ) = s s 2 + 1 + ∫ 0 ∞ e - s t [ δ ( t - π 2 ) ] d t

Passo 2

Aplique as condições iniciais, y ( 0 ) = 0 e y ' ( 0 ) = 0 .

s ² Y ( s ) + 2 s Y ( s ) + 2 Y ( s ) = s s 2 + 1 + e - s ( π / 2 )

Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):

( s 2 + 2 s + 2 ) Y ( s ) = s s 2 + 1 + e - π s / 2

Y ( s ) = s ( s 2 + 1 ) ( s 2 + 2 s + 2 ) + 1 s 2 + 2 s + 2 e - π s / 2

Passo 3

Usando frações parciais para achar a inversa:

s ( s 2 + 1 ) ( s 2 + 2 s + 2 ) = A s + B s 2 + 1 + C s + D s 2 + 2 s + 2

s = 0 :   0 = 2 B + D

s = 1 :   1 = 5 A + 5 B + 2 C + 2 D

s = 2 :   2 = 20 A + 10 B + 10 C + 5 D

s = 3 :   3 = 51 A + 17 B + 30 C + 10 D

Resolvendo, chegamos em:

A = 1 5 ,   B = 2 5 ,   C =   - 1 5 e D = - 4 5 .

Y ( s ) = ( 1 5 s + 2 5 s 2 + 1 + - 1 5 s - 4 5 s 2 + 2 s + 2 ) + 1 s 2 + 2 s + 2 e - π s / 2

Agora, basta resolver esta equação e achar sua inversa!

Y ( s ) = 1 5 s s ² + 1 + 2 5 1 s 2 + 1 - 1 5 s + 1 ( s + 1 ) 2 + 1 - 3 5 1 ( s + 1 ) 2 + 1 + 1 ( s + 1 ) 2 + 1 e - π s / 2

Chegando em:

y ( t ) = ℒ - 1 { Y ( s ) } = 1 5 [ c o s ( t )   + 2   s e n ( t ) - e - t ( c o s ( t ) + 3   s e n ( t ) ] - u π / 2 ( t ) e π 2 - t c o s ( t )

Passo 4

Abaixo está o gráfico de y(t) versus t.

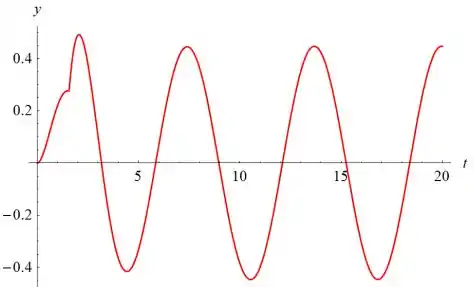
Resposta

y ( t ) = 1 5 [ c o s ( t )   + 2   s e n ( t ) - e - t ( c o s ( t ) + 3   s e n ( t ) ] - u π / 2 ( t ) e π 2 - t c o s ( t )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ' ' + 4 y = u π ( t ) - u 3 π ( t ) ;y ( 0 ) = 0 ,y ' ( 0
Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ' '+ 2 y '+ 2 y=h ( t ) ; y ( 0 )=0 ,y ' ( 0 )= 1 ; h ( t
Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ' '+ 4 y= s e n ( t )+ u π ( t )s e n ( t - π ) ;y ( 0 )=
Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ( 4 ) - 5 y ' ' + 4 y=1 - u π ( t ) ;y ( 0 ) = 0 ,y ' ( 0
Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ( 4 ) - y=u 1 ( t ) - u 2 ( t ) ;y ( 0 ) = 0 ,y ' ( 0 ) =