Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 59
Encontre o valor médio de na região .
é o triângulo com vértices , e .
Passo 1
Precisamos lembrar como calcular o valor médio de uma função em um intervalo:
Assim, precisamos calcular a área do domínio de integração e a integral da função neste domínio.
Passo 2
Neste caso, temos que o domínio de integração é o triângulo:
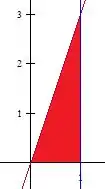
Assim, a integral pode ser escrita como
Portanto,
Passo 3
A área do domínio de integração é
Assim,
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 19-24, esboce a região de integração e calcule a integral. ∫ 0 ln 8 ∫ 0 ln y e x + y d xd y
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = 0 , x = 0 , y = 1
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = 3 - 2 x , y = x e
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = e - x , y = 1 e x
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = tg x , x = 0 e