Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 1
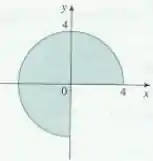
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma função qualquer contínua em .
Passo 1
Fala ai galera. A questão pede pra identificar que tipo de sistema de coordenadas é melhor para calcular a integral sobre a região dada e escrever a integral.
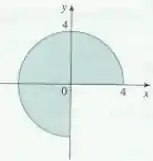
Note que a região é um trecho de círculo, de modo que é mais simples usar coordenadas polares. Lembrando que para coordenadas polares a integral vai ficar com essa cara aqui:
onde:
Então o próximo passo é identificar quais são os intervalos de e , ou seja, qual maior e menor valor que cada um poderá adotar. Cuidado, o valor de está relacionado apenas com o raio do círculo e não os pontos que ele intercepta.
Como o raio do disco é , devemos ter e para o ângulo polar, devemos ter de modo a varrer os três primeiros quadrantes. Vamos relembrar os ângulos da circunferência:
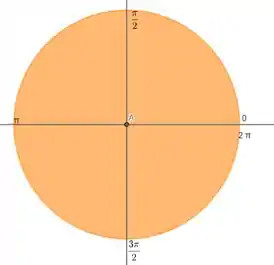
Passo 2
Escrevendo a integral com os intervalos e a função e não esquecendo do jacobiano em coordenadas polares () que está presente na fórmula, temos:
↓