Desenhe o sólido limitado pelo plano e pelo paraboloide e determine seu volume exato. (Utilize seu SCA para fazer esse desenho, para achar as equações das fronteiras da região de integração e para calcular a integral dupla.)
Passo 1
Fala, galerinha! Tudo certinho?
A questão pede pra gente conseguir o desenho do sólido limitado pelas equações:
e
E calcularmos seu volume exato.
Para esboço de superfícies de sólidos, um software muito prático de usar é o Geogebra Calculator.
Vamos ver como fica!
Passo 2
Essa é uma questão que teremos que recorrer os GeoGebra 3D Calculator para fazer esboços e calcular a integral. Fazendo um esboço das duas superfícies:
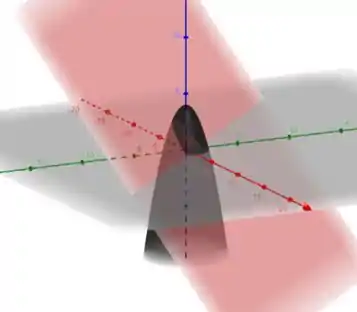
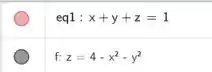
Na imagem acima estão os inputs digitados no Software.
Passo 3
Para achar as fronteiras da região de integração, vamos igualar as equações do paraboloide com o plano, porque assim a gente acha qual a interseção entre os sólidos e o plano :
Assim,
Olhando na nossa imagem lá do passo 1, podemos perceber que o formato do sólido no plano é um círculo, então vamos completar quadrados na equação que temos para chegarmos em um formato mais simples, assim a gente identifica o centro e o raio com mais facilidade:
Logo,
Desta forma, o domínio de integração será o disco com centro e raio :
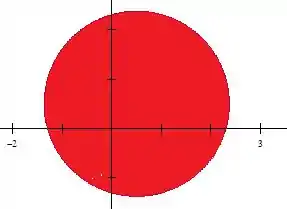
Passo 4
Isolando como função de na equação da circunferência:
Então podemos dizer que varia entre a parte positiva e a negativa dessa equação.
Já varia no intervalo
Já que o círculo está com origem em e seu raio é . Portanto,
Fazendo a integral no computador: