Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 21
Utilize coordenadas polares para determinar o volume do sólido dado.
Delimitado pelo hiperboloide e pelo plano .
Passo 1
E aí, amigos! Tranquilidade?
A questão quer o volume do sólido delimitado pelo hiperboloide e pelo plano . O volume do sólido a gente acha por:
Mas nota que faltam nossos limites de integração dessa integral, sem isso não conseguimos calculá-la. Os limites de integração do sólido são dados pela região de integração, que no nosso caso é a interseção entre o hiperboloide e o plano.
O exercício pede para expressarmos nossa integral em coordenadas polares. A relação entre coordenadas polares e retangulares é:
E:
Então, nosso procedimento deve ser o de encontrar nossos limites de integração e calculamos nossa integral do volume de forma iterada: de dentro para fora como já estamos acostumados.
Bora juntos!
Passo 2
A questão pede o volume do sólido delimitado pelo hiperboloide e pelo plano .
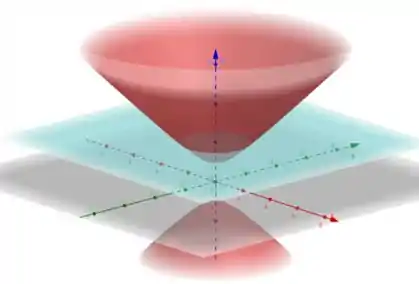
Vamos achar primeiro a interseção entre eles para assim obtermos o domínio de integração. Fazemos na equação do paraboloide:
E obtemos:
Assim, a região de integração será o disco de raio centrado na origem. Da nossa imagem acima já podemos ver que realmente a interseção do paraboloide com o plano é um disco.
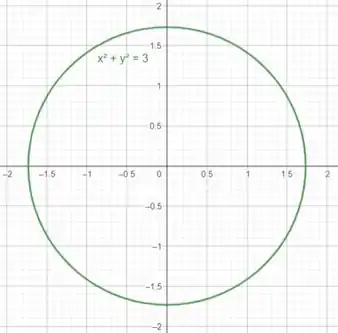
Então nossos limites de integração são:
Reescrevendo nossa função
em coordenadas polares, temos:
Então:
Além disso, vemos que o plano está acima do hiperboloide nesse domínio, de modo que
Em coordenadas polares,
Agora é partir para o cálculo da integral!
Passo 3
Podemos separar a integral do produto num produto de integrais:
Fazendo a integral em :
Aplicando os limites de integração:
Assim, basta integrarmos em :
Aplicando os limites de integração: