25. Esboçar a região de continuidade das seguintes funções:

b)

Existem funções que são sempre contínuas em seus domínios, ou seja, você não precisa fazer a análise para esses casos. Uma dessas funções é a logarítmica, desde que seja sempre positiva.

Analisando o denominador, temos:

Logo, minha função é continua em todo o domínio onde

Representando graficamente, temos:

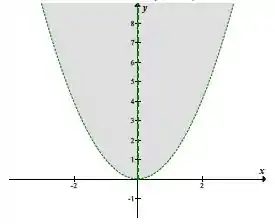
Observação: Não analisamos o numerador, pois é sempre continuo.