Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 2d

2) Esboçar a região de integração e calcular as integrais iteradas seguintes:

d) ∫ 1 e ∫ 0 ln ⁡ x 1 e - e y d y   d x

Passo 1

Pelos intervalos de integração, temos que:

0 ≤ y ≤ ln ⁡ x 1 ≤ x ≤ e

Logo o gráfico é o seguinte:

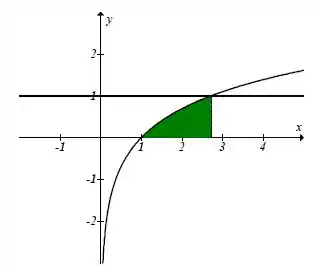
Passo 2

Para simplificar a resolução do problema, vamos inverter os limites de integração. Portanto, vamos integrar com relação a x . Trate y como uma constante no primeiro caso, por conta da primeira integral ser em relação a x .

∫ e y e 1 e - e y   d x =

1 e - e y e y e = e e - e y - e y e - e y =

= - e y + e e - e y = 1

Passo 3

Agora vamos integrar em função de y , levando em conta o valor obtido na integral de x . Assim temos:

∫ 0 1 1   d x = 1

Resposta

1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a : b )x - y
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a:m) 1 1 + x 2 + 2 x y + y 2
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a:l) x s e n( π y )
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a:j) x y 2
Utilizando o Exercício 2, calcule: c )∬ A x ln ⁡ yd x d y , onde A é o retângulo 0 ≤ x ≤ 2 , 1 ≤ y ≤ 2 .