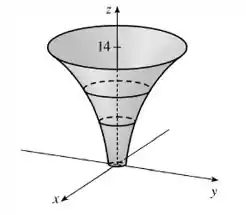
Um mapa de contorno de uma função é mostrado. Use-o para fazer um esboço aproximado do gráfico de f.
Passo 1
Olá, meu parça, vamos para mais uma resolução.
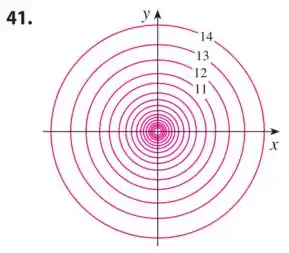
Dada a curva de nível a seguir:
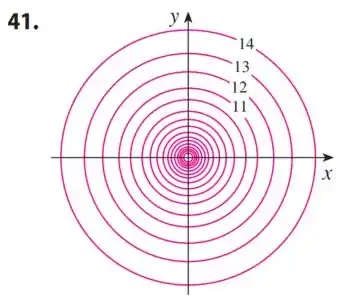
A gente vai precisar encontrar a função que gerou essa curva de nível. Para que façamos o caminho da curva de nível, ao gráfico da função, deveremos pensar em como é construída a curva de nível e alguns dos seus significados.
A curva de nível de uma função é construída com diferentes valores para e acompanhando qual equação, e consequentemente qual figura nós formamos no plano . Outra coisa a se observar na curva de nível, é o qual ‘rápido’ a curva cresce, ao nos afastarmos da origem, é interessante notar o tamanho da curva de nível.
Passo 2
Pelo mapa de contorno de uma função, vemos que o gráfico parece um tubo que é mais estreito na parte inferior e se expande cada vez mais rápido quanto mais longe estamos do plano . Daí o esboço do gráfico:
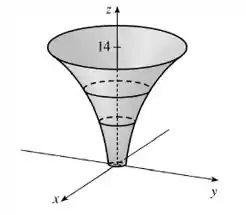
Resposta