Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 56
Se é o potencial elétrico em um ponto no plano , então as curvas de nível de são chamadas curvas equipotenciais porque em todos os pontos de tal curva o potencial elétrico é o mesmo. Esboce algumas curvas equipotenciais se , onde é uma constante positiva.
Passo 1
Eaee, belezinha??? Bom... o enunciado nos deu a seguinte equação:
Onde é uma constante positiva e é o raio do campo elétrico.
Queremos fazer o esboço de algumas curvas equipotenciais significa fazer um mapa de contorno, onde as curvas de nível são definidas pelas curvas equipotenciais.
Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível (equipotenciais).
Para isso, basta fazer e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.
Agora bora lá!! 😉
Passo 2
Igualando a função a , temos:
Reorganizando, temos:
Essa é a equação de um círculo centrado na origem.
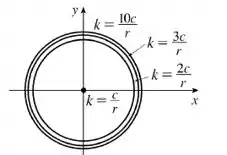
Variando , chega-se ao seguinte mapa de contorno com as equipotenciais:
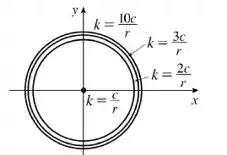
Vale notar que quando , o raio do círculo se aproxima de .
Resposta
