Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.2 - Ex. 1b
Esboce o gráfico da função dada por
Passo 1
A questão quer que esbocemos o gráfico de que é função dada por uma integral. Para isso, vamos tentar achar uma expressão fechada para ela. Integrando:
Assim,
Passo 2
Note que se trata de uma função quadrática cujo gráfico será uma parábola. Essa parábola corta o eixo vertical em e suas raízes são . A seguir segue um esboço dessa curva:
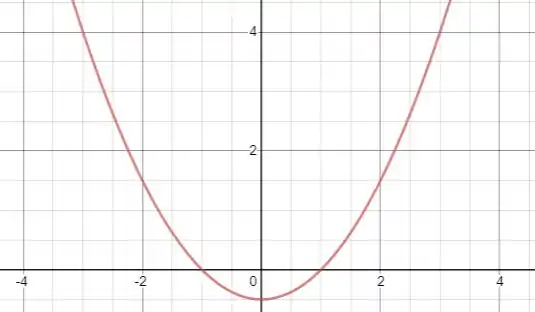
Resposta
Esboço de gráfico.
Exercícios de Livros Relacionados
O que está errado na equação? ∫ π 3 π sec θ tan θ d θ = sec θ π 3 π = - 3
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ π / 2 π c o s s e cxd x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 3 1 3 - xd x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ - 2 3 1 x 4d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 1 1 1 - x 2d x